
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


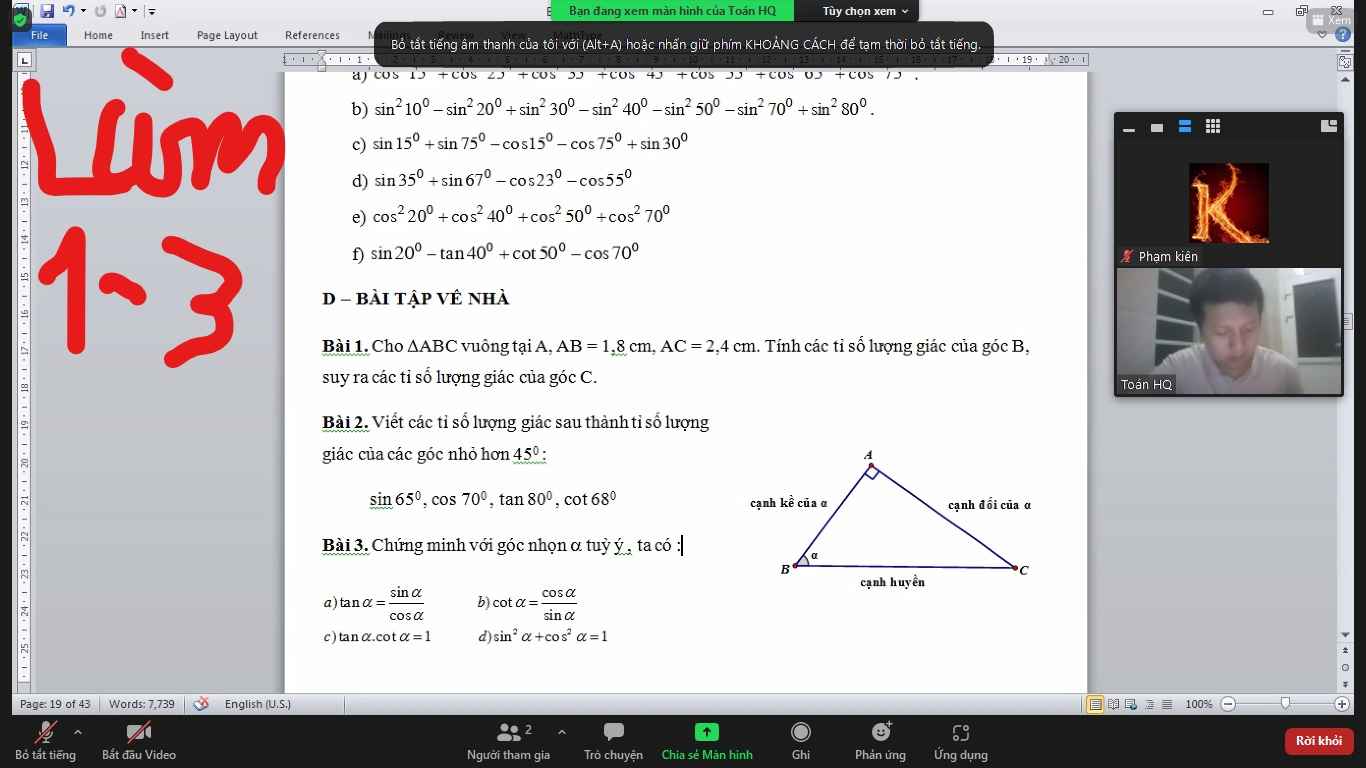
sin 650=cos 350
\(cos70^0=sin30^0\)
\(tan80^0=cot20^0\)
\(cot68^0=tan32^0\)

\(\text{Δ}=\left(-3\right)^2-4\cdot\left(2m+1\right)\)
=9-8m-4=-8m+5
Để phương trình có nghiệm kép thì -8m+5=0
hay m=5/8
Pt trở thành \(x^2-3x+\dfrac{9}{4}=0\)
hay x=3/2

Gọi vận tốc xe máy đi từ A là x (km/h); x > 28.
\(\Rightarrow\) Vận tốc xe đạp đi từ B là x - 28 (km/h).
Quãng đường xe máy đi trong 3 giờ là 3x (km).
Quãng đường xe đạp đi trong 3 giờ là 3 (x - 28) = 3x - 84 (km).
Vì hai xe xuất phát cùng lúc gặp nhau sau 3 giờ và cùng đi trên 1 quãng đường AB nên ta có phương trình:
3x - 84 + 3x = 156.
\(\Leftrightarrow\) 6x = 240.
\(\Leftrightarrow\) x = 40 (TMĐK).
Vậy vận tốc xe máy đi từ A là 40 (km/h); vận tốc xe đạp đi từ B là 40 - 28 = 12 (km/h).

a: Ta có: EC//AB
AB⊥CD
Do đó: EC⊥CD
=>ΔCED nội tiếp đường tròn đường kính CD
=>O là trung điểm của CD(Vì C,E,D cùng nằm trên đường tròn O)
=>E,O,D thẳng hàng
b: Xét (O) có
ΔAEB nội tiếp
AB là đường kính
DO đó: ΔAEB vuông tại E
Xét tứ giác AEBD có
O là trung điểm của AB
O là trung điểm của ED
Do đó: AEBD là hình bình hành
mà \(\widehat{AEB}=90^0\)
nên AEBD là hình chữ nhật

\(\sqrt{a^2+3}=\sqrt{a^2+ab+bc+ca}=\sqrt{\left(a+b\right)\left(a+c\right)}\le\dfrac{1}{2}\left(a+b+a+c\right)=\dfrac{1}{2}\left(2a+b+c\right)\)
Tương tự: \(\sqrt{b^2+3}\le\dfrac{1}{2}\left(a+2b+c\right)\) ; \(\sqrt{c^2+3}\le\dfrac{1}{2}\left(a+b+2c\right)\)
Cộng vế với vế:
\(VT\le\dfrac{1}{2}\left(4a+4b+4c\right)=2\left(a+b+c\right)\)

1.theo bất đẳng thức côsi ta có
\(a+b\ge2\sqrt{ab}\\ b+c\ge2\sqrt{ab}\\ c+a\ge2\sqrt{ab}\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge8\sqrt{ab.bc.ca}\)
\(\ge8\sqrt{a^2b^2c^2}\\ \ge8abc\)
2.\(a^4+b^2\ge2\sqrt{a^4b^2}=2a^4b^2\)
\(\dfrac{a}{a^4+b^2}\le\dfrac{a}{2a^2b}=\dfrac{1}{2ab}\)
tương tự:\(\dfrac{b}{b^4+a^2}\le\dfrac{1}{2ab}\)
\(\rightarrow\dfrac{a}{a^4+b^2}+\dfrac{b}{b^4+a^2}\le\dfrac{1}{ab}\)
dấu = xảy ra khi \(a^4=b^2\\ b^4=a^2\)\(\rightarrow a^2=b^2=1\)

Bài 1:
a) Ta có: \(A=\left(\dfrac{6+\sqrt{20}}{3+\sqrt{5}}+\dfrac{\sqrt{14}-\sqrt{2}}{\sqrt{7}-1}\right):\left(2+\sqrt{2}\right)\)
\(=\left(2+\sqrt{2}\right)\cdot\dfrac{1}{2+\sqrt{2}}\)
=1
b) Ta có: \(B=\sqrt{5-2\sqrt{6}}+\sqrt{5+2\sqrt{6}}-\dfrac{11}{2\sqrt{3}+1}\)
\(=\sqrt{3}-\sqrt{2}+\sqrt{3}+\sqrt{2}-2\sqrt{3}+1\)
=1
Bài 2:
b) Ta có: \(\sqrt{9x^2-9}+\sqrt{4x^2-4}=\sqrt{16x^2-16}+2\)
\(\Leftrightarrow3\sqrt{x^2-1}+2\sqrt{x^2-1}-4\sqrt{x^2-1}=2\)
\(\Leftrightarrow x^2-1=4\)
\(\Leftrightarrow x\in\left\{\sqrt{5};-\sqrt{5}\right\}\)




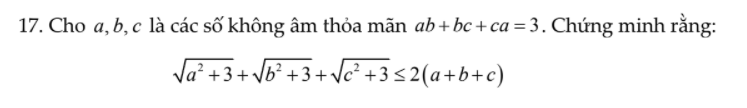 câu này với ạ! Mình cảm ơn.
câu này với ạ! Mình cảm ơn.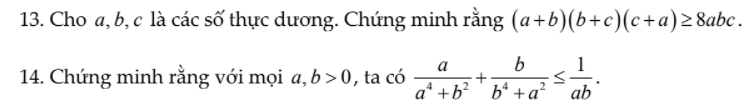




a, \(\left\{{}\begin{matrix}35x-28y=21\\35x-45y=40\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}17y=-19\\x=\dfrac{3+4y}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{19}{17}\\x=-\dfrac{13}{17}\end{matrix}\right.\)
b, Đặt x;y khác 0
Đặt 1/x = t ; 1/y = u
\(\left\{{}\begin{matrix}t-8u=18\\5t+4u=51\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5t-40u=90\\5t+4u=51\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-44u=39\\t=18+8u\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u=-\dfrac{39}{44}\\t=\dfrac{120}{11}\end{matrix}\right.\)
Theo cách đặt y = -44/39 ; x = 11/120 (tm)
\(a,\\ \Leftrightarrow\left\{{}\begin{matrix}35x-28y=21_{\left(1\right)}\\35x-45y=40_{\left(2\right)}\end{matrix}\right.\\ Lấy\left(1\right)-\left(2\right),ta.đc:\\ -17y=19\Leftrightarrow y=\dfrac{-19}{17}\\ Thay.vào.\left(1\right):\\ 35x-28.\dfrac{-19}{17}=21\Leftrightarrow x=\dfrac{-5}{17}\)
Vậy ......
\(b,\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=18+\dfrac{1}{y}\\5.\left(18+\dfrac{1}{y}\right)+\dfrac{4}{y}=51\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=18+\dfrac{1}{y}\\\dfrac{9}{y}=-39\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=18-\dfrac{13}{3}\\\dfrac{1}{y}=\dfrac{-13}{3}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{41}{3}\\\dfrac{1}{y}=\dfrac{-13}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{41}\\y=\dfrac{-3}{13}\end{matrix}\right.\)