Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`C=(sqrtx+3)/(sqrtx-2)=(sqrtx-2+5)/(sqrtx-2)=1+5/(sqrtx-2)`
Ta cần tìm `max(5/(sqrtx-2))`
Nếu `0<=x<4` thì `5/(sqrtx-2)<0`
Nếu `x>4` thì `5/(sqrtx-2)>0`
Do đó ta chỉ xét `x>4` hay `x>=5(` Do `x` nguyên `)`
`=>sqrtx-2>=sqrt5-2`
`=>5/(sqrtx-2)<=5/(sqrt5-2)`
`=>C<=1+5/(sqrt5-2)=11+sqrt5`
Vậy `C_(max)=11+sqrt5<=>x=5`

\(P=\frac{\sqrt{x}}{\sqrt{x}-1}+\frac{\sqrt{x}-2}{\sqrt{x}-1}\)
ĐKXĐ : \(\hept{\begin{cases}x\ge0\\x\ne1\end{cases}}\)
\(=\frac{\sqrt{x}+\sqrt{x}-2}{\sqrt{x}-1}\)
\(=\frac{2\sqrt{x}-2}{\sqrt{x}-1}\)
\(=\frac{2\left(\sqrt{x}-1\right)}{\sqrt{x}-1}=2\)
=> Với mọi \(\hept{\begin{cases}x\ge0\\x\ne1\end{cases}}\)thì P = 2
Đề sai à --

Vẽ hình:
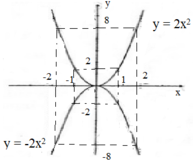
Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
a)x=-2
b) GTLN=6 khi x=0
c);x=1 bạn cần chi tiết không?