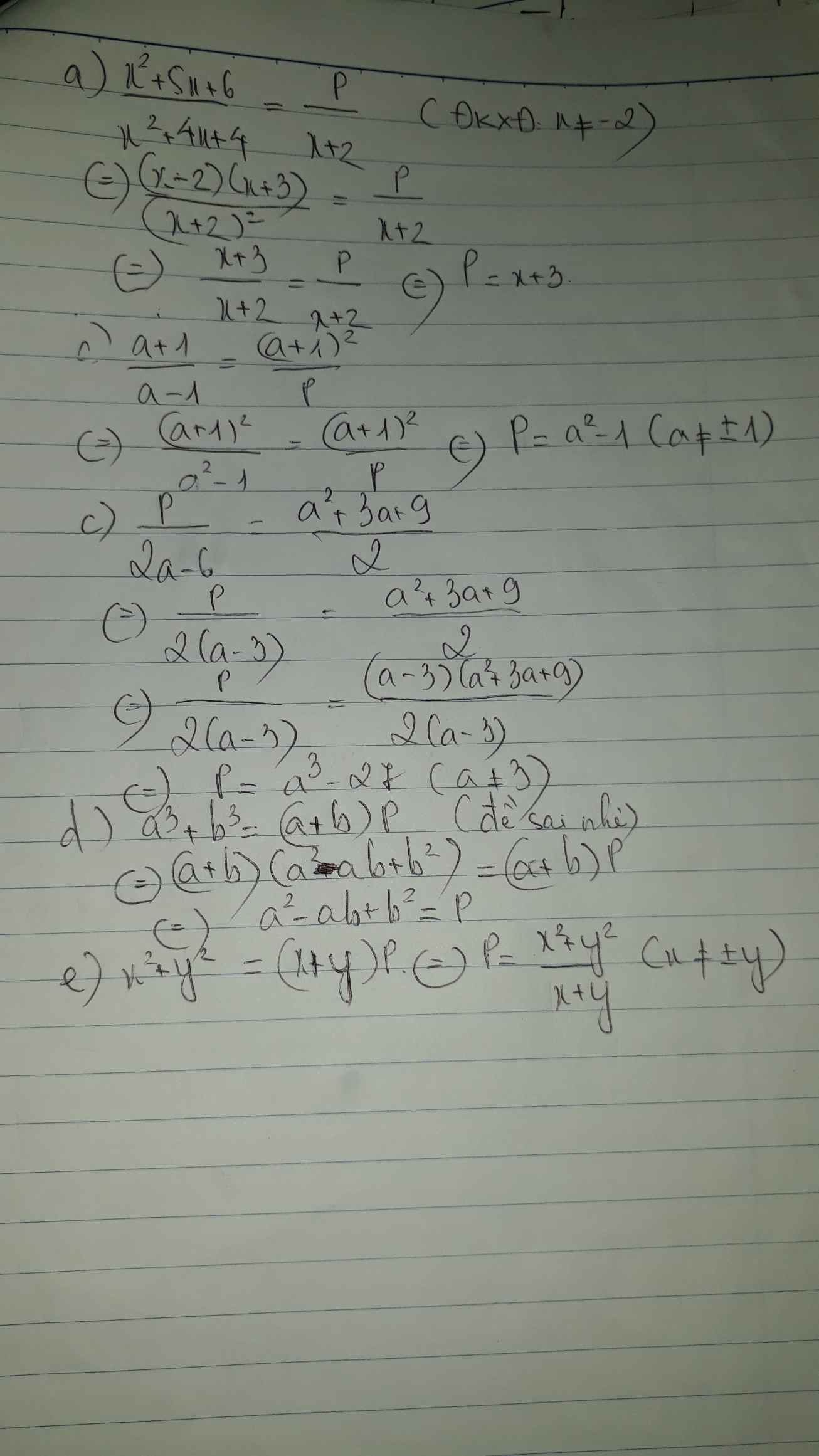NH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DD
3 tháng 9 2016
\(1.VP\)
\(\left(a+b\right)^2-2ab=a^2+2ab+b^2-2ab\)
\(=a^2+b^2=VT\left(DPCM\right)\)
LM
3 tháng 9 2016
1/ (a + b)2 - 2ab = a2 + 2ab + b2 - 2ab = a2 + b2 + (2ab - 2ab) = a2 + b2
2/ (a2 + b2)2 - 2a2b2 = a4 + 2a2b2 + b4 - 2a2b2 = a4 + b4 + (2a2b2 - 2a2b2) = a4 + b4
NB
1
VT
24 tháng 10 2019
với x+y+z=0 thì \(x^3+y^3+z^3-3xyz=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-zx\right)=0< =>\)x3 +y3 +z3 =3xyz
nếu đặt x=a2; y=b2 ;z=c2 thì ta cần có a2 +b2 +c2 =0 thì sẽ có a6 +b6 +c6 =3a2b2c2
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0< =>\frac{ab+bc+ca}{abc}=0< =>ab+bc+ca=0.\)
a+b+c=0 <=> (a+b+c)2 =0 <=> \(a^2+b^2+c^2+2\left(ab+bc+ca\right)=0< =>a^2+b^2+c^2=0.\)(chứng minh xong)
7 tháng 8 2018
a) \(a^2+b^2=\left(a+b\right)^2-2ab\)
\(VP=\left(a+b\right)^2-2ab=a^2+2ab+b^2-2ab\)\(=a^2+b^2=VT\)
\(\Rightarrowđpcm\)
b)\(a^4+b^4=\left(a^2+b^2\right)^2-2a^2b^2\)
\(VP=a^4+b^4+2a^2b^2-2a^2b^2=a^4+b^4=VT\)\(\Rightarrowđpcm\)
c) \(a^6+b^6=\left(a^2+b^2\right)\left[\left(a^2+b^2\right)^2-3a^2b^2\right]\)
\(VP=\left(a^2+b^2\right)\left(a^4-a^2b^2+b^4\right)=a^6+b^6\)
\(VP=VT\Rightarrowđpcm\)
d)\(a^6-b^6=\left(a^2-b^2\right)[\left(a^2+b^2\right)^2-a^2b^2]\)
\(VP=\left(a^2-b^2\right)\left(a^4+a^2b^2+b^4\right)=a^6-b^6=VT\)
\(VP=VT\Rightarrowđpcm\)
MG
1
3 tháng 11 2019
Một người mua một chiếc áo với giá 800000 đồng để về bán. Sau khi bán, người đó nhẩm tính số tiền lãi bằng 20% số tiền đã bỏ ra mua. 1. Tính số tiền người đó được lãi. 2. Hỏi phải tăng chiếc áo bao nhiêu tiền để được lãi bằng 20% giá bán?
14 tháng 7 2021
a) Ta có: \(\dfrac{P}{x+2}=\dfrac{x^2+5x+6}{x^2+4x+4}\)
\(\Leftrightarrow\dfrac{P}{x+2}=\dfrac{\left(x+2\right)\left(x+3\right)}{\left(x+2\right)^2}=\dfrac{x+3}{x+2}\)
hay P=x+3
31 tháng 3 2020
Ta có : \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\Leftrightarrow\frac{ab+bc+ca}{abc}=0\Leftrightarrow ab+bc+ca=0\)
\(a+b+c=0\Leftrightarrow\left(a+b+c\right)^2=0\)
\(\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=0\)
\(\Leftrightarrow a^2+b^2+c^2=0\)
Áp dụng :
\(a^3+b^3+c^3=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)+3abc\)
\(\Rightarrow a^6+b^6+c^6\)
\(=\left(a^2+b^2+c^2\right)\left(a^4+b^4+c^2-a^2b^{^2}-b^2c^2-c^2a^2\right)+3a^2b^2c^2\)
\(\Leftrightarrow a^6+b^6+c^6=3a^2b^2c^2\)
