TT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
S
29 tháng 12 2020
a) \(\dfrac{a}{5}=\dfrac{b}{4}\Rightarrow\dfrac{a^2}{25}=\dfrac{b^2}{16}\)
Áp dụng tính chất DTSBN :
\(\dfrac{a^2}{25}=\dfrac{b^2}{16}=\dfrac{a^2-b^2}{25-16}=\dfrac{1}{9}\)
\(\Rightarrow\left\{{}\begin{matrix}a^2=\dfrac{1}{9}\cdot25=\dfrac{25}{9}\\b^2=\dfrac{1}{9}\cdot16=\dfrac{16}{9}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=\dfrac{5}{3};b=\dfrac{4}{3}\\a=\dfrac{-5}{3};b=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy \(\left(a;b\right)\in\left\{\left(\dfrac{5}{3};\dfrac{4}{3}\right);\left(-\dfrac{5}{3};-\dfrac{4}{3}\right)\right\}\)
b) \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\Rightarrow\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{c^2}{16}\)
Áp dụng tính chất DTSBN :
\(\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{c^2}{16}=\dfrac{2c^2}{32}=\dfrac{a^2-b^2+2c^2}{4-9+32}=\dfrac{108}{27}=4\)
\(\Rightarrow\left\{{}\begin{matrix}a^2=4.4=16\\b^2=4.9=36\\c^2=4,16=64\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=4;=6;c=8\\a=-4;b=-6;c=-8\end{matrix}\right.\)
Vậy (a;b;c) \(\in\left\{\left(4;6;8\right);\left(-4;-6;-8\right)\right\}\)
T
2
2 tháng 11 2021
Sửa \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\)
Đặt \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=k\Rightarrow a=2k;b=3k;c=4k\)
\(a^2-b^2+2c^2=108\\ \Rightarrow4k^2-9k^2+32k^2=108\\ \Rightarrow27k^2=108\Rightarrow k^2=4\\ \Rightarrow\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=4;y=6;z=8\\x=-4;y=-6;z=-8\end{matrix}\right.\)
TH
2 tháng 11 2021
Ta có:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a^2}{2^2}=\dfrac{b^2}{3^2}=\dfrac{2c^2}{2.4^2}=\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{2c^2}{32}\)
Áp dụng tcdtsbn , ta có:
\(\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{2c^2}{32}=\dfrac{a^2-b^2+2c^2}{4-9+32}=\dfrac{108}{27}=4\)
\(\Rightarrow\left\{{}\begin{matrix}a=8\\b=12\\c=16\end{matrix}\right.\)
KJ
2
4 tháng 9 2021
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\)
\(\Rightarrow\dfrac{a^2}{4}=\dfrac{b^2}{9}=\dfrac{c^2}{16}=\dfrac{3b^2}{27}=\dfrac{2c^2}{32}=\dfrac{a^2+3b^2-2c^2}{4+27-32}=\dfrac{-16}{-1}=16\)
\(\Rightarrow\left\{{}\begin{matrix}a^2=64\\b^2=144\\c^2=256\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}a=\pm8\\b=\pm12\\c=\pm16\end{matrix}\right.\)
Vậy \(\left(a;b;c\right)\in\left\{\left(8;12;16\right),\left(-8;-12;-16\right)\right\}\)
4 tháng 9 2021
Cách khác:
Đặt \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2k\\b=3k\\c=4k\end{matrix}\right.\)
Ta có: \(a^2+3b^2-2c^2=-16\)
\(\Leftrightarrow4k^2+27k^2-32k^2=-16\)
\(\Leftrightarrow k^2=16\)
Trường hợp 1: k=4
\(\Leftrightarrow\left\{{}\begin{matrix}a=2k=8\\b=3k=12\\c=4k=16\end{matrix}\right.\)
Trường hợp 2: k=-4
\(\Leftrightarrow\left\{{}\begin{matrix}a=2k=-8\\b=3k=-12\\c=4k=-16\end{matrix}\right.\)
XO
21 tháng 2 2023
b) Ta có : \(\dfrac{2a}{3}=\dfrac{3b}{4}=\dfrac{4c}{5}\)
\(\Leftrightarrow\dfrac{a}{\dfrac{3}{2}}=\dfrac{b}{\dfrac{4}{3}}=\dfrac{c}{\dfrac{5}{4}}=\dfrac{a+b+c}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{49}{\dfrac{49}{12}}=12\)
Khi đó \(a=12.\dfrac{3}{2}=18;b=12.\dfrac{4}{3}=16;c=12.\dfrac{5}{4}=15\)
Vậy (a,b,c) = (18,16,15)
27 tháng 7 2018
a) ta có: \(\frac{a}{4}=\frac{b}{5};\frac{b}{5}=\frac{c}{8}\)
\(\Rightarrow\frac{a}{4}=\frac{b}{5}=\frac{c}{8}=\frac{5a}{20}=\frac{3b}{15}=\frac{3c}{24}\)
ADTCDTSBN
...
bn tự áp dụng rùi tìm a;b;c nha
b) ta có: \(\frac{a+3}{5}=\frac{b-2}{3}=\frac{c-1}{7}=\frac{3a+9}{15}=\frac{5b-10}{15}=\frac{7c-7}{49}\)
ADTCDTSBN
có: \(\frac{3a+9}{15}=\frac{5b-10}{15}=\frac{7c-7}{49}=\frac{3a+9-5b+10+7c-7}{15-15+49}\)
\(=\frac{\left(3a-5b+7c\right)+\left(9+10-7\right)}{49}=\frac{86+12}{49}=\frac{98}{49}=2\)
=>...
c) ta cóL \(\frac{a}{7}=\frac{b}{6}\Rightarrow\frac{a}{35}=\frac{b}{30}\)
\(\frac{b}{5}=\frac{c}{8}\Rightarrow\frac{b}{30}=\frac{c}{48}\)
\(\Rightarrow\frac{a}{35}=\frac{b}{30}=\frac{c}{48}=\frac{2b}{60}\)
ADTCDTSBN
...
các bài còn lại bn dựa vào mak lm nha!
29 tháng 11 2018
a) Theo đề, ta có:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{5}\) và a + b + c =1,5
Theo t/c của dãy tỉ số bằng nhau:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{5}=\frac{a+b+c}{2+3+5}=\frac{1,5}{10}=\frac{3}{20}\)
=>a=0,3
b=0,45
c=0,75
29 tháng 11 2018
a) Vì a,b,c tỉ lệ với 2,3,5
=> \(\frac{a}{2}=\frac{b}{3}=\frac{c}{5}\)
Áp dụng t/c dãy tỉ số bằng nhau :
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{5}=\frac{a+b+c}{2+3+5}=\frac{1,5}{10}=\frac{3}{20}\)
\(\frac{a}{2}=\frac{3}{20}=>a=\frac{3}{20}.2=\frac{3}{10}\)
\(\frac{b}{3}=\frac{3}{20}=>b=\frac{3}{20}.3=\frac{9}{20}\)
\(\frac{c}{5}=\frac{3}{20}=>c=\frac{3}{20}.5=\frac{3}{4}\)
b)
Áp dụng t/c dãy tỉ số bằng nhau :
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{a}{2}=\frac{2b}{6}=\frac{3c}{12}=\frac{a+2b-3c}{2+6-12}=\frac{-20}{-4}=5\)
\(\frac{a}{2}=5=>a=5.2=10\)
\(\frac{b}{3}=5=>b=5.3=15\)
\(\frac{c}{4}=5=>c=5.4=20\)
c) \(\frac{a}{2}=\frac{b}{3},\frac{b}{5}=\frac{c}{4}\)
\(\frac{a}{10}=\frac{b}{15},\frac{b}{15}=\frac{c}{12}\)
\(=>\frac{a}{10}=\frac{b}{15}=\frac{c}{12}\)
Áp dụng t/c dãy tỉ số bằng nhau
\(\frac{a}{10}=\frac{b}{15}=\frac{c}{12}=\frac{a+b-c}{10+15-12}=\frac{-39}{13}=-3\)
\(\frac{a}{10}=-3=>-3.10=-30\)
\(\frac{b}{15}=-3=>-3.15=-45\)
\(\frac{c}{12}=-3=>-3.12=-36\)
PT
1
CM
20 tháng 1 2018
Ta có:
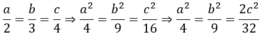
Theo tính chất dãy tỉ số bằng nhau ta có:
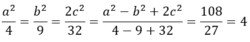
Ta có:
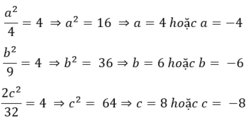
Mà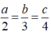 
nên a, b và c cùng dấu.
Vậy ta tìm được các số a1 = 4; b1 = 6; c1 = 8 hoặc a2 = -4; b2 = -6 và c2 = -8
79484-31949