Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
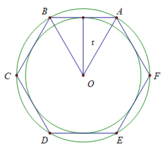
b) Cách vẽ lục giác đều có tất cả các đỉnh nằm trên đường tròn (O)
Vẽ các dây cung AB = BC = CD = DE = EF = FA = R = 2 cm
(Ta đã nêu được cách chia đường tròn thành sáu cung bằng nhau tại bài tập 10 SGK trang 71)
c) Vì các dây cung AB = BC = CD = DE = EF = FA bằng nhau nên khoảng cách từ O đến các dây là bằng nhau ( định lý liên hệ giữa dây cung và khoảng cách từ tâm đến dây)

Cách vẽ lục giác đều có tất cả các đỉnh nằm trên đường tròn (O)
Vẽ các dây cung AB = BC = CD = DE = EF = FA = R = 2 cm
(Ta đã nêu được cách chia đường tròn thành sáu cung bằng nhau tại bài tập 10 SGK trang 71)

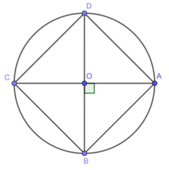
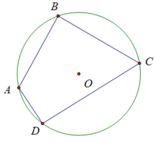
*Cách vẽ:
- Vẽ đường tròn tâm O bán kính 1,5cm
- Vẽ hai đường kính AC và BD vuông góc với nhau
- Nối AB, BC , CD, DA lại với nhau ta được hình vuông ABCD nội tiếp trong đường tròn (O; 1,5)
*Chứng minh:
Ta có : OA = OC , OB =OD
Suy ra ABCD là hình bình hành
Mặt khác : AC = BD và AC ⊥ BD
Suy ra ABCD là hình vuông

a: góc ABK=1/2*sđ cung AK=1/2*180=90 độ
=>BK vuông góc AB
=>BK//CH
góc ACK=1/2*sđ cung AK=1/2*180=90 độ
=>CE vuông góc AB
=>CH//BK
mà BK//CH
nên BHCK là hình bình hành
b: Vì M là trung điểm của BC nên M là trung điểm của HK
G là trọng tâm của ΔABC nên AG=2/3AM
=>G là trọng tâm của ΔAHK
=>H,G,O thẳng hàng

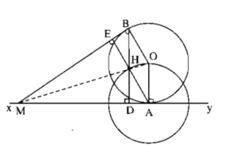
Tứ giác AOBH có BH // OA, AH // OB và OA = OB nên là hình thoi.