Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\dfrac{\left(3+\dfrac{2}{15}+\dfrac{1}{5}\right):\dfrac{5}{2}}{\left(5+\dfrac{3}{7}-2-\dfrac{1}{4}\right):\left(4+\dfrac{43}{56}\right)}\)
\(=\dfrac{\dfrac{10}{3}\cdot\dfrac{2}{5}}{\dfrac{89}{28}:\dfrac{267}{56}}=\dfrac{4}{3}:\dfrac{2}{3}=2\)
\(B=\dfrac{\dfrac{6}{5}:\left(\dfrac{6}{5}\cdot\dfrac{5}{4}\right)}{\dfrac{8}{25}+\dfrac{2}{25}}=\dfrac{\dfrac{6}{5}:\dfrac{3}{2}}{\dfrac{2}{5}}=2\)
Do đó: A=B

A = (\(\dfrac{5}{6}\) - \(\dfrac{4}{5}\)) . 1\(\dfrac{1}{5}\) + \(\dfrac{3}{16}\) : (\(\dfrac{-1}{2}\))3
A = \(\dfrac{1}{30}\) . \(\dfrac{6}{5}\) + \(\dfrac{3}{16}\) : \(\dfrac{-1}{8}\)
A = \(\dfrac{1}{25}\) + \(\dfrac{3}{16}\) . \(\dfrac{-8}{1}\)
A = \(\dfrac{1}{25}\) + \(\dfrac{-3}{2}\)
A = \(\dfrac{-73}{50}\)
B = \(\dfrac{4}{17}\) . (7\(\dfrac{3}{4}\) - 6\(\dfrac{1}{3}\)) + (5\(\dfrac{3}{4}\) - 6.95) : (-1\(\dfrac{3}{5}\))
B = \(\dfrac{4}{17}\) . \(\dfrac{17}{12}\) + (\(\dfrac{23}{4}\) - \(\dfrac{139}{20}\)) : \(\dfrac{-8}{5}\)
B = \(\dfrac{1}{3}\) + \(\dfrac{-6}{5}\) . \(\dfrac{-5}{8}\)
B = \(\dfrac{13}{12}\)

A = \(\dfrac{\left(\dfrac{47}{15}+\dfrac{3}{15}\right):\dfrac{5}{2}}{\left(\dfrac{38}{7}-\dfrac{9}{4}\right):\dfrac{267}{56}}=\dfrac{\dfrac{10}{3}.\dfrac{2}{5}}{\dfrac{89}{28}.\dfrac{56}{267}}=2\)
B= \(\dfrac{1,2:\left(\dfrac{6}{5}.\dfrac{5}{4}\right)}{0,32+\dfrac{2}{25}}=\dfrac{\dfrac{6}{5}:\dfrac{3}{2}}{\dfrac{8}{25}+\dfrac{2}{25}}=\dfrac{4}{\dfrac{5}{\dfrac{2}{5}}}=2\)
=> A = B

a: \(M=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}+\dfrac{2}{99\cdot101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{10}-\dfrac{3}{202}=\dfrac{150}{101}\)
b: 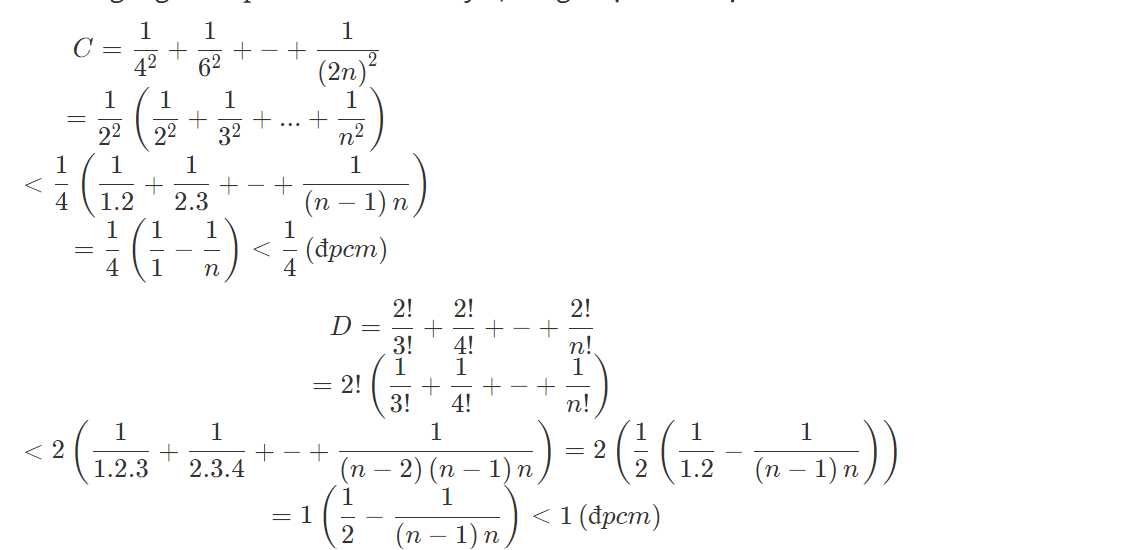

a) `1/3 - 1/4 : 2/5 = 1/3 - 5/8 = -7/24`
b) `6/7-(5/6+1/3)-(2/3+1/7) = 6/7-5/6-1/3-2/3-1/7`
`=(6/7-1/7)-(1/3+2/3)-5/6`
`=5/7-1-5/6`
`=-47/42`
c) `-5/9 . 2/5 + 4 5/9 + 5/9 . (-3/5)`
`= -5/9 . 2/5 + 4 + 5/9 + (-5/9) . 3/5`
`=-5/9 . (2/5 + 3/5-1) + 4`
`=-5/9 . 0 +4`
`=4`
d) 3 1/2 - (5 4/7 - 1 1/2) : 0,75`
`=7/2 - (39/7 - 3/2) : 3/4`
`= 7/2 - 57/14 : 3/4`
`=7/2 - 38/7`
`=-27/14`

Câu 1:
a) \(-\dfrac{2}{3}\left(x-\dfrac{1}{4}\right)=\dfrac{1}{3}\left(2x-1\right)\)
\(\Rightarrow-\dfrac{2}{3x}+\dfrac{1}{6}=\dfrac{2}{3}x-\dfrac{1}{3}\)
\(\Rightarrow\dfrac{2}{3}x+\dfrac{2}{3}x=\dfrac{1}{6}+\dfrac{1}{3}\)
\(\Rightarrow x.\left(\dfrac{2}{3}+\dfrac{2}{3}\right)=\dfrac{1}{2}\)
\(\Rightarrow x.\dfrac{4}{3}=\dfrac{1}{2}\)
\(\Rightarrow x=\dfrac{1}{2}:\dfrac{4}{3}\)
\(\Rightarrow x=\dfrac{3}{8}\)

\(a.\dfrac{2}{3}+\dfrac{4}{3}:\dfrac{-2}{3}=\dfrac{2}{3}+\left(-2\right)=\dfrac{-4}{3}\)
\(b.3\dfrac{4}{5}-\left(2\dfrac{1}{4}+1\dfrac{4}{5}\right)\\ =3\dfrac{4}{5}-2\dfrac{1}{4}-1\dfrac{4}{5}\\ =\left(3\dfrac{4}{5}-1\dfrac{4}{5}\right)-2\dfrac{1}{4}\\ =2-2\dfrac{1}{4}=\dfrac{1}{4}\)
\(c.\dfrac{-3}{5}.\dfrac{4}{7}+\dfrac{3}{7}.\dfrac{-3}{5}+\dfrac{3}{5}\\ =\dfrac{-3}{5}\left(\dfrac{4}{7}+\dfrac{3}{7}\right)+\dfrac{3}{5}\\ =\dfrac{-3}{5}+\dfrac{3}{5}=0\)
a) \(\dfrac{2}{5}+\dfrac{4}{3}:\dfrac{-2}{3}\)
\(=\dfrac{2}{5}+\dfrac{4}{3}.\dfrac{-3}{2}\)
\(=\dfrac{2}{5}+-2\)
\(=\dfrac{2}{5}+\dfrac{-10}{5}\)
\(=\dfrac{-8}{5}\)

Câu 2:
\(\Leftrightarrow x\left(\dfrac{1}{6}+\dfrac{1}{10}+\dfrac{1}{15}+...+\dfrac{1}{78}\right)=\dfrac{220}{39}\)
\(\Leftrightarrow2x\left(\dfrac{1}{12}+\dfrac{1}{20}+...+\dfrac{1}{156}\right)=\dfrac{220}{39}\)
\(\Leftrightarrow x\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{12}-\dfrac{1}{13}\right)=\dfrac{110}{39}\)
\(\Leftrightarrow x\cdot\dfrac{10}{39}=\dfrac{110}{39}\)
=>x=11
Bài 1:
Ta có:
\(\left(100a+3b+1\right)\left(2^a+10a+b\right)=225\left(1\right)\)
Mà \(225\) lẻ nên \(\left\{{}\begin{matrix}100a+3b+1\\2^a+10a+b\end{matrix}\right.\) cùng lẻ \(\left(2\right)\)
\(*)\) Với \(a=0\) ta có:
Từ \(\left(1\right)\Leftrightarrow\left(100.0+3b+1\right)\left(2^a+10.0+b\right)=225\)
\(\Leftrightarrow\left(3b+1\right)\left(1+b\right)=225=3^2.5^2\)
Do \(3b+1\div3\) dư \(1\) và \(3b+1>1+b\)
Nên \(\left(3b+1\right)\left(1+b\right)=25.9\) \(\Rightarrow\left\{{}\begin{matrix}3b+1=25\\1+b=9\end{matrix}\right.\) \(\Leftrightarrow b=8\)
\(*)\) Với \(a\ne0\left(a\in N\right)\) ta có:
Khi đó \(100a\) chẵn, từ \(\left(2\right)\Rightarrow3b+1\) lẻ \(\Rightarrow b\) chẵn
\(\Rightarrow2^a+10a+b\) chẵn, trái với \(\left(2\right)\) nên \(b\in\varnothing\)
Vậy \(\left\{{}\begin{matrix}a=0\\b=8\end{matrix}\right.\)
Bài 2:
Ta có:
\(A=\dfrac{1}{1+3}+\dfrac{1}{1+3+5}+...+\dfrac{1}{1+3+...+2017}\)
\(=\dfrac{1}{\dfrac{\left(1+3\right).2}{2}}+\dfrac{1}{\dfrac{\left(1+5\right).3}{2}}+...+\dfrac{1}{\dfrac{\left(1+2017\right).1009}{2}}\)
\(=\dfrac{2}{2.4}+\dfrac{2}{3.6}+\dfrac{2}{4.8}+...+\dfrac{2}{1009.2018}\)
\(=\dfrac{1}{2.2}+\dfrac{1}{3.3}+\dfrac{1}{4.4}+...+\dfrac{1}{1009.1009}\)
\(\Rightarrow A< \dfrac{1}{2.2}+\left(\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{1008.1009}\right)\)
\(\Rightarrow A< \dfrac{1}{4}+\left(\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{1008}-\dfrac{1}{1009}\right)\)
\(\Rightarrow A< \dfrac{1}{4}+\left(\dfrac{1}{2}-\dfrac{1}{1009}\right)\)
\(\Rightarrow A< \dfrac{1}{4}+\dfrac{1}{2}=\dfrac{3}{4}\) (Đpcm)
Tuyệt cú mèo

