Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ét hai n-giác đều: A1A2..An và A'1A'2..A'n
=> số đo các góc đều bằng nhau = 180(n-2)/n
hai tgiác A1A2A3 và A'1A'2A'3 bằng nhau
=> tồn tại duy nhất phép dời D: (A1A2A3) --> (A'1A'2A'3)
do phép dời bảo toàn độ lớn của góc (kể cả hướng góc) và khoảng cách 2 điểm
=> qua D: A4 --> A'4
Có thể làm rõ hơn là gọi D: A4 --> A''4
có A3A4 = A'3A''4 và góc định hướng A2Â3A4 = A'2Â'3A''4
=> A''4 ≡ A'4
tương tự qua D: An --> A'n
=> D: (A1A2..An) --> (A'1A'2..A'n)
=> A1A2..An = A'1A'2..A'n

Chọn D
Cách 1:
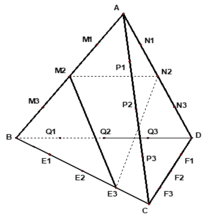
Gọi các điểm được đánh dấu để chia đều các cạnh của tứ diện đều ABCD như hình vẽ.
+ Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu.
Số phần tử của S là số cách chọn ra 3 điểm không thẳng hàng trong số 18 điểm đã cho.
Chọn ra 3 điểm trong 18 điểm trên: có C 18 3 cách.
Chọn ra 3 điểm thẳng hàng trong 18 điểm trên có 6. C 6 3 = 6 cách.
Suy ra số tam giác thỏa mãn là C 18 3 - 6 = 810
+ Gọi T là tập hợp các tam giác lấy từ ABCD sao cho mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện ABCD.
- Chọn 1 cạnh của tứ diện để mặt phẳng chứa tam giác chỉ song song với đúng cạnh đó: có C 6 1 cách.
Xét các tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD, suy ra tam giác đó phải có một cạnh song song với BD.
- Có 6 cách chọn cạnh song song với BD là
![]()
- Giả sử ta chọn cạnh M 2 N 2 là cạnh của tam giác. Cần chọn đỉnh thứ 3 của tam giác trong 16 điểm còn lại.
Do M 2 N 2 ⊂ (ABD) mà mặt phẳng chứa tam giác song song với BD nên đỉnh thứ 3 không thể là 7 điểm còn lại nằm trong mp(ABD).
Do mặt phẳng chứa tam giác chỉ song song với BD nên đỉnh thứ 3 không được trùng với một trong ba điểm E 2 , F 2 , P 2 . Vậy đỉnh thứ 3 chỉ được chọn trong 16 -7 - 3 = 6 điểm còn lại.
Suy ra có 6 tam giác có 1 cạnh là M 2 N 2 và mặt phẳng chứa nó chỉ song song với BD.
Vậy số tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD là: 6.6 = 36.
Tương tự cho các trường hợp khác, ta có số tam giác mà mặt phẳng chứa nó chỉ song song với đúng một cạnh của tứ diện ABCD là: 36.6 = 216.
Vậy xác suất cần tìm là
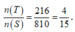
Cách 2: Lưu Thêm
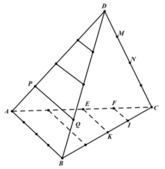
+) Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu.
Chọn ra 3 điểm trong 18 điểm trên: có C 18 3 cách.
Trong số C 18 3 đó, có 6 cách chọn ra 3 điểm thẳng hàng trên các cạnh.
Suy ra n(S) = C 18 3 - 6 = 810
+) Xét phép thử: “Lấy ngẫu nhiên một phần thử thuộc S”. Ta có ![]()
+) Gọi T là biến cố: “Mặt phẳng chứa tam giác được chọn song song với đúng một cạnh của tứ diện đã cho”.
Chọn một cạnh của tứ diện: 6 cách, (giả sử chọn AB).
Chọn đường thẳng song song với AB: 6 cách, (giả sử chọn PQ).
Chọn đỉnh thứ 3: 6 cách, (M, N, E, K, F, I).
Suy ra n(T) = 6.6.6 = 216
Vậy 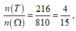

Do \(d\perp\left(ABC\right)\) nên \(MN\perp BC\)
\(\left\{{}\begin{matrix}MC\perp\left(BOH\right)\\BN\subset\left(BOH\right)\end{matrix}\right.\) \(\Rightarrow MC\perp BN\)
\(\left\{{}\begin{matrix}MB\perp\left(CHO\right)\\CN\subset\left(CHO\right)\end{matrix}\right.\)\(\Rightarrow MB\perp CN\)
