Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

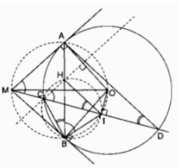

A, B, I nhìn MO cố định dưới một góc bằng 90° nên A, B, I nằm trên đường tròn bán kính MO.
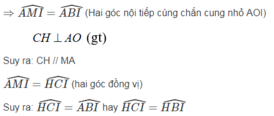
B và C cùng nằm trên một nửa mặt phẳng bờ chứa đường HI tạo với HI một góc bằng nhau nên tứ giác BCHI nội tiếp.


Bạn tự vẽ hình nhé
a.Xét 2 tam giác vuông ABO và ACO có
BO=CO (đều là BK đường tròn)
AB=AC (Độ dài hai tiếp tuyến của một đường tròn cùng xuất phát từ một điểm bên ngoài đường tròn thì bằng nhau)
góc ABO=góc ACO=90 độ
Suy ra tam giác ABO=tam giác ACo (c.g.c) suy ra góc BAO=góc CAO
Tam giác ABC cân tại A nên AO vừa là phân giác của góc BAC vừa là đường cao của tam giác ABC hạ từ A xuống BC vậy AO vuông góc với BC
b\()\)Ta có góc BCO=góc CAO (cùng phụ với góc AOC)
góc CAO=góc BAO
suy ra góc BCO=góc BAO (1)
Xét tam giác vuông BCH có góc CBH+góc BCO=90 độ (2)
Ta có góc ABC+góc BAO=90 độ (3)
Từ (1) (2) (3) suy ra góc CBH=góc ABC nên BC là phân giác của góc ABH
c,Gọi G là giao của BD và AC
\(\Delta DCG\)có OA \(//DG\)\((\)cùng \(\perp BC\)\()\); OD=OC
=> A là trung điểm của GC
Có BH//AC, theo hệ quả của định lý Thales:
\(\frac{BI}{AG}=\frac{ID}{IA}=\frac{IH}{AC}\)
=> IH=IB(đpcm)
Chúc bạn học tốt

a.Xét 2 tam giác vuông ABO và ACO có
BO=CO (đều là BK đường tròn)
AB=AC (Độ dài hai tiếp tuyến của một đường tròn cùng xuất phát từ một điểm bên ngoài đường tròn thì bằng nhau)
góc ABO=góc ACO=90 độ
Suy ra tam giác ABO=tam giác ACo (c.g.c) suy ra góc BAO=góc CAO
Tam giác ABC cân tại A nên AO vừa là phân giác của góc BAC vừa là đường cao của tam giác ABC hạ từ A xuống BC vậy AO vuông góc với BC
c,Ta có góc BCO=góc CAO (cùng phụ với góc AOC)
góc CAO=góc BAO
suy ra góc BCO=góc BAO (1)
Xét tam giác vuông BCH có góc CBH+góc BCO=90 độ (2)
Ta có góc ABC+góc BAO=90 độ (3)
Từ (1) (2) (3) suy ra góc CBH=góc ABC nên BC là phân giác của góc ABH
mình chỉ biết làm câu a và c thôi mong bạn thông cảm

a: Vì A,B,D,C cùng nằm trên (O)
nên ABDC nội tiếp
b: Xét (D) có
MB,MF là tiếp tuyến
=>MB=MF
Xét (D) có
NF,NC là tiếp tuyến
=>NF=NC
=>MB+CN=MF+NF=MN