K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
4
NH
17 tháng 6 2019
\(D=\frac{3}{1.3}+\frac{3}{3.5}+...+\frac{3}{199.201}\)
\(D=\frac{3}{2}\left(\frac{2}{1.3}+\frac{2}{3.5}+...+\frac{2}{199.201}\right)\)
\(D=\frac{3}{2}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{199}-\frac{1}{201}\right)\)
\(D=\frac{3}{2}\left(1-\frac{1}{201}\right)\)
\(D=\frac{3}{2}.\frac{200}{201}\)
\(D=\frac{100}{67}\)
T
17 tháng 6 2019
#)Giải :
\(D=\frac{3}{1.3}+\frac{3}{3.5}+\frac{3}{5.7}+...+\frac{3}{199.201}\)
\(D=\frac{3}{2}\left(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{199.201}\right)\)
\(D=\frac{3}{2}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{199}-\frac{1}{201}\right)\)
\(D=\frac{3}{2}\left(1-\frac{1}{201}\right)\)
\(D=\frac{3}{2}\times\frac{200}{201}\)
\(D=\frac{100}{67}\)
TA
2
HP
12 tháng 5 2016
\(A=\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+.....+\frac{1}{2013.2015}\)
\(=\frac{1}{2}.\left(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+......+\frac{2}{2013.2015}\right)\)
\(=\frac{1}{2}.\left(\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+....+\frac{1}{2013}-\frac{1}{2015}\right)\)
\(=\frac{1}{2}.\left(1-\frac{1}{2015}\right)=\frac{1}{2}.\frac{2014}{2015}=\frac{1007}{2015}\)
Vậy A=1007/2015
TN
12 tháng 5 2016
\(2A=2\left(\frac{1}{1.3}+\frac{1}{3.5}+...+\frac{1}{2013.2015}\right)\)
\(2A=1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{2013}-\frac{1}{2015}\)
\(2A=1-\frac{1}{2015}\)
\(A=\frac{2014}{2015}:2\)
\(A=\frac{1007}{2015}\)
12 tháng 5 2016
1/1.3+1/3.5+...+1/2013.2015
=1/2.(1/1-1/3+1/3-1/5+...+1/2013-1/2015)
=1/2.(1/1-1/2015)
=1/2.2014/2015
=1007/2015
12 tháng 5 2016
A=1/1.3+1/3.5+1/5.7+...+1/2013.2015
2A=2.(1/1.3+1/3.5+1/5.7+...+1/2013.2015)
=2/1.3+2/3.5+2/5.7+...+2/2013.2015
=1-1/3+1/5-1/7+1/7-1/9+...+1/2013-1/2015
=1-1/2015
=2014/2015
=>2A=2014/2015=>A=1007/2015
PM
6
11 tháng 5 2019
A = 1/1.3 + 1/3.5 + 1/5.7 + ... + 1/2011.2013
A = 1/2.(2/1.3 + 2/3.5 + 2/5.7 + ... + 2/2011.2013)
A = 1/2.(1 - 1/3 + 1/3 - 1/5 + 1/5 - 1/7 + ... + 1/2011 - 1/2013)
A = 1/2.(1 - 1/2013)
A = 1/2.2012/2013
A = 1006/2013
11 tháng 5 2019
\(A=\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{2011.2013}\)
\(2A=\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{2011.2013}\)
\(2A=1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{2011}-\frac{1}{2013}\)
\(2A=1+\left(\frac{1}{3}-\frac{1}{3}\right)+\left(\frac{1}{5}-\frac{1}{5}\right)+\left(\frac{1}{7}-\frac{1}{7}\right)+...+\left(\frac{1}{2011}-\frac{1}{2011}\right)-\frac{1}{2013}\)
\(2A=1-\frac{1}{2013}\)
\(2A=\frac{2012}{2013}\)
\(A=\frac{2012}{2013}:2\)
\(A=\frac{1006}{2013}\)
~ Hok tốt ~
NT
6
BT
2
Q
6 tháng 3 2017
a) \(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{99.101}\)
\(=1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}-...-\frac{1}{99}-\frac{1}{101}\)
\(=1-\frac{1}{101}\)
\(=\frac{100}{101}\)
b) \(\frac{7}{1.3}+\frac{7}{3.5}+\frac{7}{5.7}+...+\frac{7}{99.101}\)
\(=7.\left(\frac{1}{1.3}+\frac{1}{3.5}+\frac{7}{5.7}+...+\frac{7}{99.101}\right)\)
\(=7.\frac{1}{7}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{99}-\frac{1}{101}\right)\)
\(=\frac{7}{7}\left(1-\frac{1}{101}\right)\)
\(=\frac{100}{101}\)
DB
1
22 tháng 3 2021
S= 1/1.3 + 1/3.5 + 1/5.7 +................+ 1/200.202
=>S=1/2.(2/1.3+2/3.5+2/5.7+...+2/200.202)
=>S=1/2.(3-1/1.3+5-3/3.5+...+202-200/200.202)
=>S=1/2.(1-1/3+1/3-1/5+...+1/200-1/202)
=>S=1/2.(1-1/202)
=>S=1/2.201/202
=>S=201/404
Vậy S=201/404
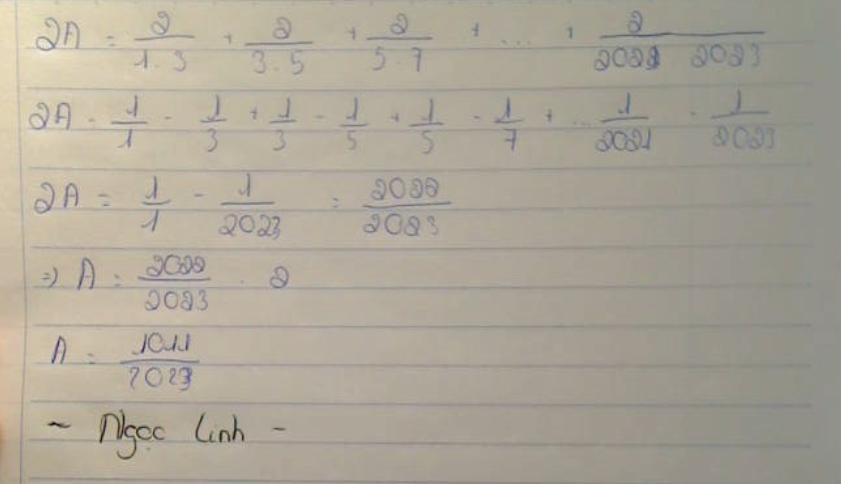
\(A=\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{199.201}\).
\(2A=\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{199.201}\)
\(2A=\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{199}-\frac{1}{201}\)
\(2A=\frac{1}{1}-\frac{1}{201}\)
\(2A=\frac{201-1}{201}\)
\(2A=\frac{200}{201}\)
\(A=\frac{200}{201}:2\)
\(A=\frac{200}{402}\)
Đáp số là 100/201