HA
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
3 tháng 12 2017
Sử dụng tính chất nếu a b < 1 thì a b < a + m b + m với mọi a, b, m ∈ Z
A = 10 10 + 1 10 11 + 1 < 10 10 + 10 10 11 + 10 = 10 9 + 1 10 10 + 1 = B
Vậy A < B
Cách khác: 10A= 10 11 + 10 10 11 + 1 = 1 + 9 10 11 + 1
10 B = 10 10 + 10 10 10 + 1 = 1 + 9 10 11 + 1 mà 9 10 11 + 1 < 9 10 10 + 1 => A < B
PT
1
PT
1
NL
0
ND
2
PT
1
CM
16 tháng 1 2019
a, 7 8 + 7 9 + 7 10 = 7 8 . 1 + 7 + 7 2 = 7 8 . 57 ⋮ 57
b, 10 10 - 10 9 - 10 8 = 10 8 . ( 10 2 - 10 - 1 ) = 10 8 . 89 ⋮ 89
c, 64 10 - 32 11 - 16 3 = ( 2 6 ) 10 - ( 2 5 ) 11 - ( 2 4 ) 13 = 2 60 - 2 55 - 2 52 = 2 52 2 8 - 2 3 - 1
= 2 52 . 247 = 2 52 . 13 . 19 ⋮ 19
HT
0
27 tháng 8 2020
\(a,\frac{8}{9}< \frac{108}{109}\)
\(b,\frac{97}{100}< \frac{98}{99}\)
\(c,\frac{19}{18}>\frac{2017}{2016}\)
\(d,\frac{15}{16}>\frac{515}{616}\)
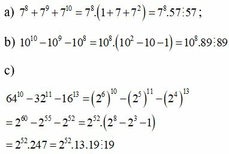
\(taco\)
\(A=\frac{10^8+1}{10^9+1}\Rightarrow10A=1+\frac{9}{10^9+1}\)
\(B=\frac{10^9+1}{10^{10}+1}\Rightarrow10B=1+\frac{9}{10^{10}+1}\)
\(Vì:\frac{9}{10^9+1}>\frac{9}{10^{10}+1}\Rightarrow10A>10B\Rightarrow A>B\)
Ta có:
\(A=\frac{10^8+1}{10^9+1}\Leftrightarrow10A=\frac{10^9+10}{10^9+1}=\frac{10^9+1+9}{10^9+1}=1+\frac{9}{10^9+1}\)
\(B=\frac{10^9+1}{10^{10}+1}\Leftrightarrow10B=\frac{10^{10}+10}{10^{10}+1}=\frac{10^{10}+1+9}{10^{10}+1}=1+\frac{9}{10^{10}+1}\)
Vì \(\frac{9}{10^9+1}>\frac{9}{10^{10}+1}\)nên \(1+\frac{9}{10^9+1}>1+\frac{9}{10^{10}+1}\)
\(\Rightarrow10A>10B\)\(\Rightarrow A>B\)
Vậy A>B