K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
WK
1
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2023
Đặt \(3^x=t>0\Rightarrow t^2-2\left(7-x\right)t+45-18x=0\)
\(\Delta'=\left(7-x\right)^2-\left(45-18x\right)=\left(x+2\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}t=7-x+x+2=9\\t=7-x-\left(x+2\right)=5-2x\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}3^x=9\Rightarrow x=2\\3^x=5-2x\left(1\right)\end{matrix}\right.\)
Xét (1) \(\Leftrightarrow3^x+2x-5=0\)
Nhận thấy \(x=1\) là 1 nghiệm của (1)
Xét hàm \(f\left(x\right)=3^x+2x-5\Rightarrow f'\left(x\right)=3^x.ln3+2>0;\forall x\)
\(\Rightarrow f\left(x\right)\) đồng biến trên R nên \(f\left(x\right)\) có tối đa 1 nghiệm
\(\Rightarrow x=1\) là nghiệm duy nhất của (1)
Vậy pt đã cho có 2 nghiệm thực \(x=\left\{1;2\right\}\)
DT
2
14 tháng 4 2016
\(1+\log_2\left(9^x-6\right)=\log_2\left(4.3^x-6\right)\)
Điều kiện : \(\begin{cases}9^x>6\\3^x>\frac{3}{2}\end{cases}\) \(\Leftrightarrow x>\log_96\)
\(1+\log_2\left(9^x-6\right)=\log_2\left(4.3^x-6\right)\Leftrightarrow9^x-2.3^x-3=0\)
\(\Leftrightarrow\begin{cases}3^x=-1\\3^x=3\end{cases}\) \(\Leftrightarrow3^x=3\Leftrightarrow x=1\) (thỏa mãn điều kiện)
Kết luận \(x=1\)
18 tháng 8 2018
Điều kiện xác định : 3\(^x\)>2
Ta có: \(\log_2\left(4.3^x-6\right)=\log_2\left(2\sqrt{2}\right).\log_{2\sqrt{2}}\left(4.3^x-6\right)\)
\(\log_2\left(4.3^x-6\right)-\dfrac{3}{2}\log_{2\sqrt{2}}\left(9^x-6\right)=1\left(1\right)\)\(\Leftrightarrow\log_2\left(2\sqrt{2}\right)\log_{2\sqrt{2}}\left(4.3^x-6\right)-\dfrac{3}{2}\log_{2\sqrt{2}}\left(9^x-6\right)=1\)
\(\Rightarrow\dfrac{3}{2}\log_{2\sqrt{2}}\left(4.3^x-6\right)-\dfrac{3}{2}\log_{2\sqrt{2}}\left(9^x-6\right)=1\)\(\Leftrightarrow\dfrac{3}{2}[\log_{2\sqrt{2}}\left(4.3^x-6\right)-\log_{2\sqrt{2}}\left(9^X-6\right)]=1\)
\(\Leftrightarrow\log_{2\sqrt{2}}\left(\dfrac{4.3^X-6}{9^X-6}\right)=\dfrac{2}{3}\)\(\Leftrightarrow\log_{2\sqrt{2}}\left(\dfrac{4.3^X-6}{9^X-6}\right)=\log_{2\sqrt{2}}\left(2\right)\)
\(\Leftrightarrow\dfrac{4.3^X-6}{9^X-6}=2\Leftrightarrow4.3^X-6=2.9^X-12\)\(\Leftrightarrow2.(3^X)^2-4.3^X-6=0\Rightarrow\left[{}\begin{matrix}3^X=3\left(TM\right)\\3^X=-1\left(loai\right)\end{matrix}\right.\)
\(\Rightarrow x=1.\)Vậy x=1 là nghiệm của phương trình (1)
LT
0
QN
1
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2020
Bạn coi lại đề câu a, chỗ \(\log_5-x\) đó
b.
\(\Leftrightarrow9^x-3^x-2.3^x-2=0\)
\(\Leftrightarrow3^x\left(3^x-1\right)-2\left(3^x-1\right)=0\)
\(\Leftrightarrow\left(3^x-2\right)\left(3^x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3^x=2\\3^x=1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\log_32\\x=0\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 3 2023
\(\int\limits^9_0f\left(x\right)dx=F\left(9\right)-F\left(0\right)\)
\(\Rightarrow F\left(9\right)-F\left(0\right)=9\)
\(\Rightarrow F\left(9\right)=9+F\left(0\right)=9+3=12\)
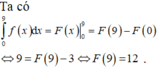
9x - 4.3x -45 = 0
(3x)2 - 4.3x - 45 = 0
đặt 3x = t >0 ta có
t2 -4t - 45 = 0
Δ = (-42) - 4.(-45)
Δ = 16 + 180 = 196
\(\left[{}\begin{matrix}t_1=9\\t_2=-5(loại)\end{matrix}\right.\)
3x = 9 ⇒x = 2