Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

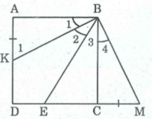
Trên tia đối của tia CD lấy điểm M sao cho CM = AK
Ta có: AK + CE = CM + CE = EM (1)
Xét ∆ ABK và ∆ CBM, ta có:
AB = CB (gt)
∠ A = ∠ C = 90 0
AK = CM (theo cách vẽ)
Suy ra: ∆ ABK = ∆ CBM (c.g.c)
⇒ ∠ B 1 = ∠ B 4 (2)
Lại có: ∠ B 1 = ∠ B 2 ( do BK là tia phân giác của ABE)
Suy ra: ∠ B 1 = ∠ B 2 = ∠ B 4
Mà ∠ (KBC) = 90 0 - ∠ B 1 (3)
Tam giác CBM vuông tại C nên: ∠ M = 90 0 - ∠ B 4 (4)
Từ (2), (3) và (4) suy ra: ∠ (KBC) = ∠ M (5)
Hay ∠ B 2 + ∠ B 3 = ∠ M
⇒ ∠ B 4 + ∠ B 3 = ∠ M( vì ∠ B 2 = ∠ B 4 )
Hay: ∠ (EBM) = ∠ M
⇒ ∆ EBM cân tại E ⇒ EM = BE. (6)
Từ (1) và (6) suy ra: AK + CE = BE.

trên tia đối của AD lấy N sao cho AN = CE
ta có:
Δ BCE = Δ BAN (2 cạnh góc vuông = nhau)
=> CBE^ = ABN^ (1)
BK là phân giác của ABE^ nên:
KBE^ = KBA^ (2)
(1) + (2) được:
CBE^ + KBE^ = ABN^ + KBA^
=> CBK^ = KBN^ (*)
mà: CBK^ = BKN^ (**) ( so le trong)
(*) và (**) => BKN^ = KBN^ => BNK là tam giác cân tại N
=> NB = NK
=> NB = AN + AK = CE + AK (3)
do: Δ BCE = Δ BAN => BE = NB (4)
(3) và (4) => CE + AK = BE

trên tia đối của AD lấy N sao cho AN = CE
ta có:
Δ BCE = Δ BAN (2 cạnh góc vuông = nhau)
=> CBE^ = ABN^ (1)
BK là phân giác của ABE^ nên:
KBE^ = KBA^ (2)
(1) + (2) được:
CBE^ + KBE^ = ABN^ + KBA^
=> CBK^ = KBN^ (*)
mà: CBK^ = BKN^ (**) ( so le trong)
(*) và (**) => BKN^ = KBN^ => BNK là tam giác cân tại N
=> NB = NK
=> NB = AN + AK = CE + AK (3)
do: Δ BCE = Δ BAN => BE = NB (4)
(3) và (4) => CE + AK = BE
ta có:
Δ BCE = Δ BAN (2 cạnh góc vuông = nhau)
=> CBE^ = ABN^ (1)
BK là phân giác của ABE^ nên:
KBE^ = KBA^ (2)
(1) + (2) được:
CBE^ + KBE^ = ABN^ + KBA^
=> CBK^ = KBN^ (*)
mà: CBK^ = BKN^ (**) ( so le trong)
(*) và (**) => BKN^ = KBN^ => BNK là tam giác cân tại N
=> NB = NK
=> NB = AN + AK = CE + AK (3)
do: Δ BCE = Δ BAN => BE = NB (4)
(3) và (4) => CE + AK = BE
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
li-ke cho minhf nhes bn Nguyễn Thị Thùy Trang

Trên tia đối của AD lấy N sao cho AN = CE
Ta có:
Δ BCE = Δ BAN (2 cạnh góc vuông = nhau)
=> CBE= ABN (1)
BK là phân giác của ABE nên:
KBE = KBA (2)
(1) + (2) được:
CBE + KBE = ABN + KBA
=> CBK = KBN(3)
mà: CBK= BKN(4) ( so le trong)
(3) và (4) => BKN = KBN => BNK là tam giác cân tại N
=> NB = NK
=> NB = AN + AK = CE + AK (3)
do: Δ BCE = Δ BAN => BE = NB (4)
(5) và (6) => CE + AK = BE

1. \(\Delta AFD=\Delta AFH\left(ch-gn\right)\Rightarrow AD=AH=a\)
2. \(\Delta AKH=\Delta AKB\left(ch-cgv\right)\Rightarrow\widehat{KAH}=\widehat{KAB}\) hay \(\widehat{KAE}=\widehat{KAB}\)
AK là tia phân giác của góc BAE
3. \(\Delta AFD=\Delta AFH\left(cmt\right)\Rightarrow FD=FH\)
\(\Delta AKH=\Delta AKB\left(cmt\right)\Rightarrow HK=KB\)
Chu vi tam giác CFK là:
\(FK+KC+FC=FH+HK+KC+FC=FD+KB+KC+FC=\left(FD+FC\right)+\left(KB+KC\right)=DC+BC=2a\)

Gọi giao điểm của IK và FE là O
ΔIOE và ΔFOK cùng vuông tại O có:
DE chung
IEOˆ=OFKˆ (vì IE // CD)
ΔIOE = ΔFOK (cgv - gnk)
=> IE = KF (tương ứng)
Có: F,KϵCDF,KϵCD mà IE // CD => KF // IE
Xét tứ giác FIEK có:
IE // KF (cmt)
IE = KF (cmt)
FIEK là hình bình hành (dhnb) có 2 đường chéo IK ⊥⊥ FE (gt) \Rightarrow FIEK là hình thoi
