Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
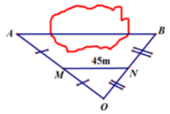
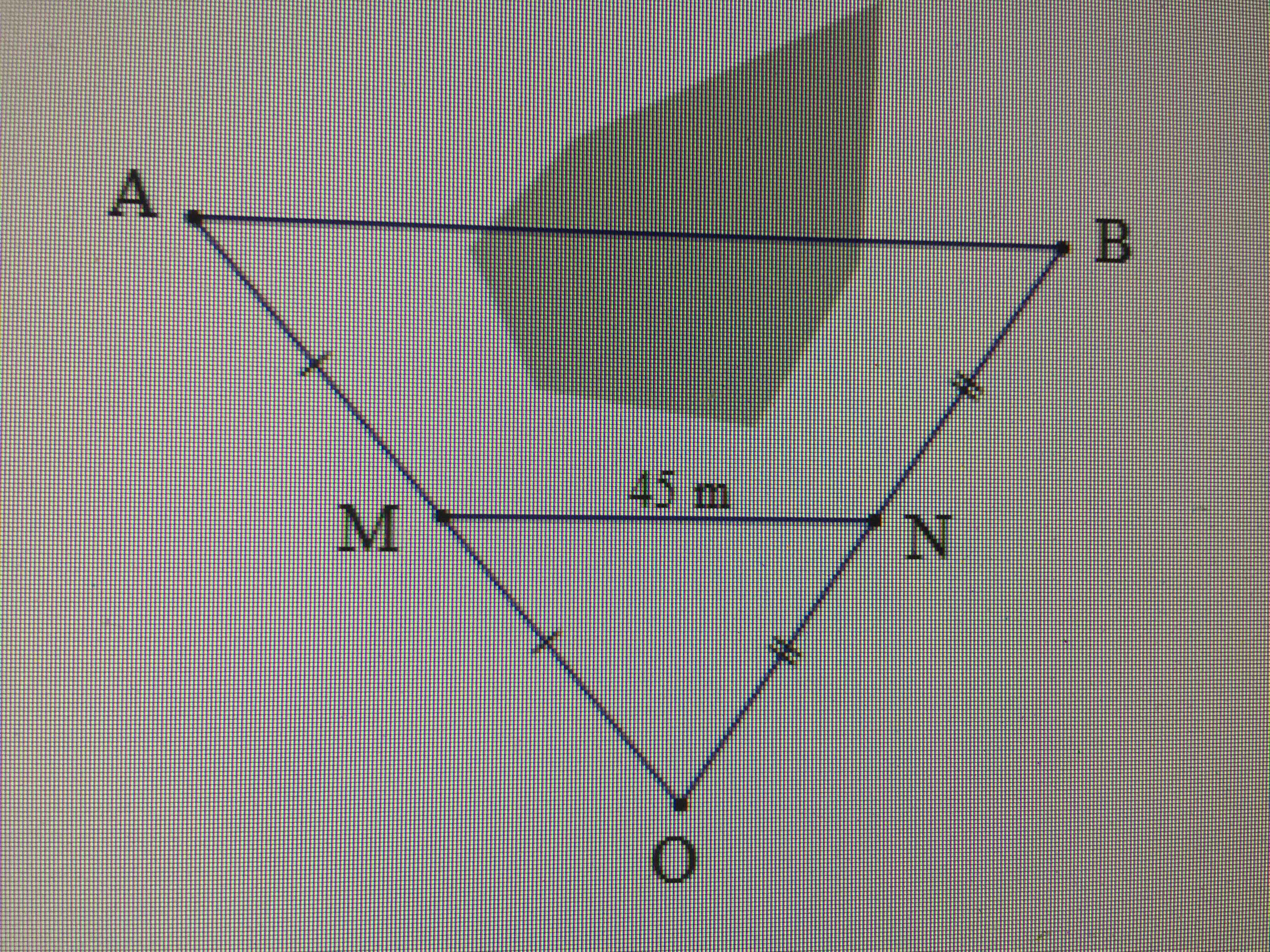
Xét tam giác OAB có:
M là trung điểm AO(gt)
N là trung điểm OB(gt)
=> MN là đường trung bình
\(\Rightarrow AB=2MN=2.45=90\left(m\right)\)
Xét ΔABC có
M là trung điểm của BC
N là trung điểm của AB
Do đó: MN là đường trung bình
=>MN=AC/2
hay AC=50m
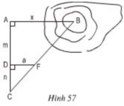
a) Cách đo:
+ Tạo một tia Ay trên mặt đất vuông góc với tia AB.
+ Trên tia Ay lấy điểm C bất kì.
+ Chọn điểm F sao cho F nằm giữa B và C.
+ Từ F hạ FD vuông góc với AC (D nằm trên AC).
+ Đo các cạnh AD, DC, DF ta tính được khoảng cách AB.
b) ΔCDF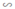 
ΔCAB (do DF // AB)
a) Cách đo:
+ Tạo một tia Ay trên mặt đất vuông góc với tia AB.
+ Trên tia Ay lấy điểm C bất kì.
+ Chọn điểm F sao cho F nằm giữa B và C.
+ Từ F hạ FD vuông góc với AC (D nằm trên AC).
+ Đo các cạnh AD, DC, DF ta tính được khoảng cách AB.
b) ΔCDF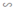 
ΔCAB (do DF // AB)
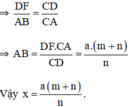
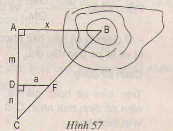
a) Cách đo:
- Chọn thêm hai điểm D và C sao cho A, D, C thẳng hàng và AC ⊥ AB.
- Chọn điểm B sao cho C, F, B thẳng hàng và DF ⊥ AC.
Giải:
a) Cách đo: Chọn thêm hai điểm C và D sao cho A,D,C thẳng hàng AC ⊥ AB.
- Chọn điểm B sao cho C, F, B thằng hàng và DF ⊥ AC.
b) ∆CDF ∽ ∆CAB (DF // AB)
=> DFAB=CDCADFAB=CDCA = > AB = DF.CACD=a(m+n)mDF.CACD=a(m+n)m
vẫy x= DF.CACD=a(m+n)mDF.CACD=a(m+n)m
