Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a) Ax ⊥ OA tại A, By ⊥ OB tại B nên Ax, By là các tiếp tuyến của đường tròn.
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
CM = CA; DM = DB;
∠O1 = ∠O2; ∠O3 = ∠O4
⇒ ∠O2 + ∠O3 = ∠O1 + ∠O4 = 1800/2 = 900 (tính chất hai tia phân giác của hai góc kề bù).
⇒ ∠OCD = 900
b) CM và CA là hai tiếp tuyến của đường tròn, cắt nhau tại C nên CM = CA
Tương tự:
DM = DB
⇒ CM + DM = CA + DB
⇒ CD = AC + BD.
c) Ta có OM ⊥ CD
Trong tam giá vuông COD, OM Là đường cao thuộc cạnh huyển
OM2 = CM.DM
Mà OM = OA = OA = AB/2 và CM = AC; DM = BD
Suy ra AC.BD = AB2/2 = không đổi

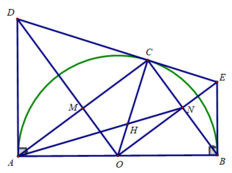
d) Ta có: N là trung điểm của BC
⇒ AN là trung tuyến của ΔABC
CO cũng là trung tuyến của ΔABC
AN ∩ CO = H
⇒ H là trọng tâm ΔABC
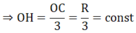
Vậy khi C di chuyển trên nửa đường tròn (O) thì H di chuyển trên nửa đường tròn
(O; R/3)

a: Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: CM=CA và OC là tia phân giác của góc MOA(1)
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB và OD là tia phân giác của góc MOB(2)
Từ (1) và (2) suy ra \(\widehat{COD}=\dfrac{1}{2}\left(\widehat{MOA}+\widehat{MOB}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
hay ΔCOD vuông tại O
b: Xét ΔCOD vuông tại O có OM là đường cao
nên \(MC\cdot MD=MO^2=R^2=AC\cdot BD\)

Xét (O) có
CM,CA là các tiếp tuyến
nên CM=CA và OC là phân giác của góc MOA(1)
mà OM=OA
nên OC là đường trung trực của MA
=>OC vuông góc với MA tại I
Xét (O) có
DM,DB là các tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
mà OM=OB
nên OD là trung trực của BM
=>OD vuông góc với BM
Từ (1) và (2) suy ra góc COD=1/2*180=90 độ

Bạn tự vẽ hình nhé :
1.Vì CM,CA là tiếp tuyến của (O)
\(\Rightarrow CM\perp OM,CA\perp OA\)
\(\Rightarrow CAOM\)nội tiếp đường tròn đường kính OC
Tương tự DMOB nội tiếp đường tròn đường kính OD
2 . Vì CM,CA là tiếp tuyến của (O)
\(\Rightarrow CM=CA,OC\) là phân giác \(\widehat{AOM}\)
Tương tự DM = DB , OD là phân giác ^BOM
Mà \(\widehat{AOM}+\widehat{MOB}=180^0\)
\(\Rightarrow OC\perp OD\)
Lại có ; \(OM\perp CD\Rightarrow CM.DM=OM^2\Rightarrow CM.DM=R^2\)
Mà : \(CM=CA,DM=DB\Rightarrow AC.BD=R^2\Rightarrow AC.3R=R^2\Rightarrow AC=\frac{R}{3}\)
\(\Rightarrow S_{ABCD}=\frac{1}{2}AB\left(BD+CA\right)=\frac{1}{2}.2R.\left(3R+\frac{R}{3}\right)=\frac{10R^2}{3}\)
3.Vì CM,CA là tiếp tuyến của (O)
\(\Rightarrow CO\perp AM=E\) là trung điểm AM
Tương tự \(OD\perp BM=F\) là trung điểm BM
\(\Rightarrow MN\) là đường trung bình \(\Delta ABC\Rightarrow EF//MN\)
Mà \(OE\perp ME,OF\perp MF,MN\perp ON\)
\(\Rightarrow M,E,N,O,F\in\) đường tròn đường kính OM
\(\Rightarrow EFNO\) nội tiếp
\(\Rightarrow\widehat{EFO}+\widehat{ENO}=180^0\)
Mà \(\widehat{NEF}+\widehat{ENO}=180^0\) ( EF // AB => EF//NO )
\(\Rightarrow EFON\) là hình thang cân