
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu 3:
a. $y^2+2y+1=(y+1)^2$
b. $9x^2+y^2-6xy=(3x)^2-2.3x.y+y^2=(3x-y)^2$
c. $25a^2+4b^2+20ab=(5a)^2+2.5a.2b+(2b)^2$
$=(5a+2b)^2$
d. Sửa đề:
$x^2-x+\frac{1}{4}=x^2-2.x.\frac{1}{2}+(\frac{1}{2})^2$
$=(x-\frac{1}{2})^2$
Câu 5:
a. $x(x-2)+x-2=0$
$\Leftrightarrow x(x-2)+(x-2)=0$
$\Leftrightarrow (x-2)(x+1)=0$
$\Leftrightarrow x-2=0$ hoặc $x+1=0$
$\Leftrightarrow x=2$ hoặc $x=-1$
b.
$5x(x-3)-x+3=0$
$\Leftrightarrow 5x(x-3)-(x-3)=0$
$\Leftrightarrow (x-3)(5x-1)=0$
$\Leftrightarrow x-3=0$ hoặc $5x-1=0$
$\Leftrightarrow x=3$ hoặc $x=\frac{1}{5}$

Bài 3:
a: Xét ΔAEB và ΔADC có
\(\widehat{A}\) chung
\(\widehat{ABE}=\widehat{ACD}\)
Do đó; ΔAEB\(\sim\)ΔADC
Suy ra: AE/AD=AB/AC
hay \(AE\cdot AC=AB\cdot AD\)
b: Xét ΔODB và ΔOEC có
\(\widehat{OBD}=\widehat{OCE}\)
\(\widehat{DOB}=\widehat{EOC}\)
Do đó:ΔODB\(\sim\)ΔOEC
Suy ra: OD/OE=OB/OC
hay \(OD\cdot OC=OB\cdot OE\)
c: Xét ΔADE và ΔACB có
AD/AC=AE/AB
\(\widehat{A}\) chung
Do đó:ΔADE\(\sim\)ΔACB

a) Ta có: \(6x^4-9x^3\)
\(=3x^3\cdot2x-3x^3\cdot3\)
\(=3x^3\left(2x-3\right)\)
b) Ta có: \(x^2y^2z+xy^2z^2+x^2yz^2\)
\(=xyz\cdot\left(xy+yz+xz\right)\)
c) Ta có: \(2x\left(x+3\right)+2\left(x+3\right)\)
\(=2\cdot\left(x+3\right)\cdot x+2\cdot\left(x+3\right)\cdot1\)
\(=2\left(x+3\right)\left(x+1\right)\)
d) Ta có: \(\left(x+5\right)^2-3\left(x+5\right)\)
\(=\left(x+5\right)\left(x+5-3\right)\)
\(=\left(x+5\right)\left(x+2\right)\)
e) Ta có: \(2x\left(x-3\right)-\left(x-3\right)^2\)
\(=\left(x-3\right)\left(2x-x+3\right)\)
\(=\left(x-3\right)\left(x+3\right)\)
a, 6x4 - 9x3 = 3x3 (2x-3x) = 3x3 (-x) = -3x4
b, x2y2z + xy2z2 + x2yz2 = xyz (xy+yz+xz)
c, 2x (x+3) + 2 (x+3) = (x+3) (2x+2) = (x+3) 2 (x+1)
d, (x+5)2 - 3 (x+5) = (x+5) (x+5-3) = (x+5) (x+2)
e, 2x (x-3) - (x-3)2 = (x-3) [2x-(x-3)] = (x-3) (2x-x+3) = (x-3) (x+3) = x2 - 9
Tự làm á! Đúng sai thì chịu
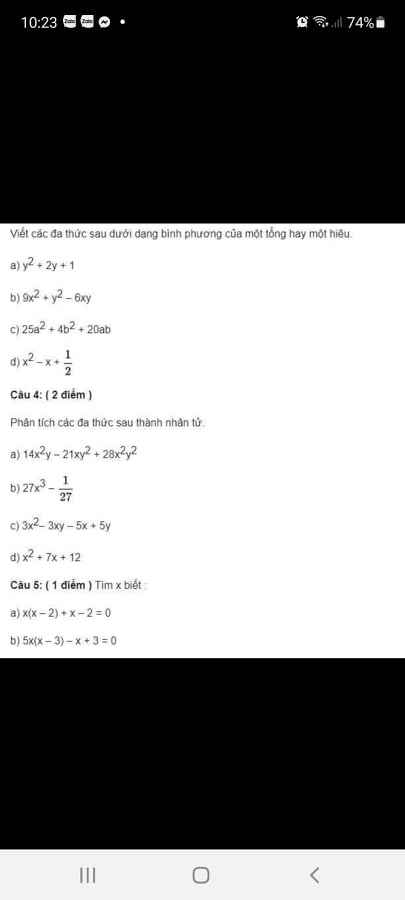

\(5-\left(6-x\right)=4\left(3-2x\right)\)
\(5-6+x=12-8x\)
\(-1+x=12-8x\)
\(x-1=12-8x\)
\(12+1=8x+1\)
\(8x=13-1\)
\(x=12:8\)
\(x=\dfrac{12}{8}=\dfrac{3}{2}\)
\(PT\Leftrightarrow5-6+x=12-8x\)
\(\Leftrightarrow9x=13\)
\(\Leftrightarrow x=\dfrac{13}{9}\)
Vậy: \(S=\left\{\dfrac{13}{9}\right\}\)