
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



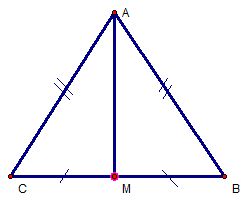
a) Xét 2 \(\Delta\) \(ABM\) và \(ACM\) có:
\(AB=AC\left(gt\right)\)
\(BM=CM\) (vì M là trung điểm của \(BC\))
Cạnh AM chung
=> \(\Delta ABM=\Delta ACM\left(c-c-c\right)\)
=> \(\widehat{BAM}=\widehat{CAM}\) (2 góc tương ứng)
=> \(AM\) là đường phân giác của \(\widehat{A}.\)
b) Xét \(\Delta ABC\) có:
\(AB=AC\left(gt\right)\)
=> \(\Delta ABC\) cân tại A.
Có \(AM\) là đường phân giác (cmt) đồng thời \(AM\) cũng là đường cao của \(\Delta ABC.\)
=> \(AM\) là đường cao của \(\Delta ABC.\)
c) Theo câu b) ta có \(\Delta ABC\) cân tại A.
Có \(AM\) là đường cao đồng thời \(AM\) cũng là đường trung trực của \(\Delta ABC.\)
=> \(AM\) là đường trung trực của \(BC.\)
Chúc bạn học tốt!

Mình nghĩ đề bài phải là \(\Delta ABC\) cân tại A chứ. Hoàng Thùy Linh
gọi a,b,c là độ dại 3 cạnh,ha,hb,hc là 3 đường cao tương ứng
ha = 4 và hb = 12,ta tìm hc
+ ta có
S = 1/2*a.ha
=>a = 2S/ha
tương tự
b = 2S/hb
và
c=2S/hc
+ do ABC la 1 tam giác nên
* a + b > c
=> 2S/ha + 2S/hb > 2S/hc
<> 1/hc < 1/4 + 1/12 = 1/3
=> hc > 3
* b + c > a
=> 1/12 + 1/hc > 1/4
<>1/hc > 1/6
=> hc < 6
do hc nguyên nên hc = 4 hoạc hc = 5
Thay a = x cho dễ
Ta có :
4a/2 = 12b/2 = xc/2 = S (S là diện tích tam giác)
=> a = 2 ; b = 6 ; c = 2S /x
Do x - y < z < x + y (bất đẳng thức trong tam giác)
=> S/2 - S/6 < 2S/x < S/2 + S/6
=> 2S /6 < 2S /x < 2S/3 . Mà x thuộc Z
=> x = {4 ,5}