Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Vẽ hình giúp mình với,mình cần gấp.
a: Xét ΔHAO vuông tại A và ΔHIO vuông tại I có
OH chung
góc AOH=góc IOH
=>ΔHAO=ΔHIO
b: H là tâm đường tròn nội tiếp ΔKOB
=>d(H,BK)=HA=4cm
Ta có :\(\left(\frac{3}{2}-\frac{5}{11}-\frac{3}{13}\right).\left(2x-2\right)=\left(-\frac{3}{4}+\frac{5}{22}+\frac{3}{26}\right)\)
=> \(\left(\frac{3}{2}-\frac{5}{11}-\frac{3}{13}\right).\left(2x-2\right)=-\frac{1}{2}\left(\frac{3}{2}-\frac{5}{11}-\frac{3}{13}\right)\)
=> \(2x-2=-\frac{1}{2}\)
=> \(2x=\frac{3}{2}\)
=> \(x=\frac{3}{4}\)
Câu 8: D.\(\dfrac{4}{5}x^4y^7\)
Câu 9:
\(7x^2y^3+8x^2y^3-2x^2y^3+M=10x^2y^3\)
\(M=\) \(10x^2y^3-7x^2y^3-8x^2y^3+2x^2y^3\)
\(M=\left(10-7-8+2\right)x^2y^3\) \(=-3x^2y^3\)
Vậy: M là \(-3x^2y^3\)
Câu 10: MIK KHÔNG BIẾT LÀM CÂU NÀY XIN LỖI NHA
Câu 11:
a) \(A\left(x\right)=x^5-3x^2+7x^4-9x^3+7x^2+2x\)
\(A\left(x\right)=x^5+\left(-3x^2+7x^2\right)+7x^4-9x^3+2x\)
\(A\left(x\right)=x^5+4x^2+7x^4-9x^3+2x\)
\(A\left(x\right)=x^5+7x^4-9x^3+4x^2+2x\)
- Hệ số cao nhất: 1 (Vì \(x^5=1x^5\) mà \(x^5\) có bậc cao nhất, nên 1 là hệ số cao nhất)
- Hệ số tự do không có (Vì những số nào có bậc là 0 mới là hệ số tự do. Ví dụ: 2,6,...)
\(B\left(x\right)=5x^4-x^5+x^2-2x^3+3x^2+3\)
\(B\left(x\right)=5x^4-x^5+(x^2+3x^2)-2x^3+3\)
\(B\left(x\right)=5x^4-x^5+4x^2-2x^3+3\)
\(B\left(x\right)=-x^5+5x^4-2x^3+4x^2+3\)
- Hệ số cao nhất: \(-1\)
- Hệ số tự do: 3
NHỮNG CHỖ NÀO IN ĐẬM VÀ NGHIÊNG KHÔNG GHI NHÁ
Lời giải:
ĐKĐB $\Rightarrow \frac{2}{c}=\frac{a+b}{ab}\Rightarrow c(a+b)=2ab$
Khi đó:
$\frac{a}{b}-\frac{a-c}{c-b}=\frac{a(c-b)-b(a-c)}{b(c-b)}=\frac{ac-ab-ab+bc}{b(c-b)}=\frac{c(a+b)-2ab}{b(c-b)}=\frac{2ab-2ab}{b(c-b)}=0$
$\Rightarrow \frac{a}{b}=\frac{a-c}{c-b}$ (đpcm)
c. \(\left|\dfrac{8}{4}-\left|x-\dfrac{1}{4}\right|\right|-\dfrac{1}{2}=\dfrac{3}{4}\)
\(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{8}{4}-x+\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{8}{4}+x-\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{9}{4}-x\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{7}{4}+x\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}\dfrac{9}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\\x=\dfrac{9}{4}-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\\\left[{}\begin{matrix}\dfrac{7}{4}+x-\dfrac{1}{2}=\dfrac{3}{4}\\-\dfrac{7}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\end{matrix}\right.\\\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-3\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\\x=-3\end{matrix}\right.\)
Ở nơi x=9/4-1/2 là x-9/4-1/2 nha
a. -1,5 + 2x = 2,5
<=> 2x = 2,5 + 1,5
<=> 2x = 4
<=> x = 2
b. \(\dfrac{3}{2}\left(x+5\right)-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{3}{2}x+\dfrac{15}{2}-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{9x}{6}+\dfrac{45}{6}-\dfrac{3}{6}=\dfrac{8}{6}\)
<=> 9x + 45 - 3 = 8
<=> 9x = 8 + 3 - 45
<=> 9x = -34
<=> x = \(\dfrac{-34}{9}\)
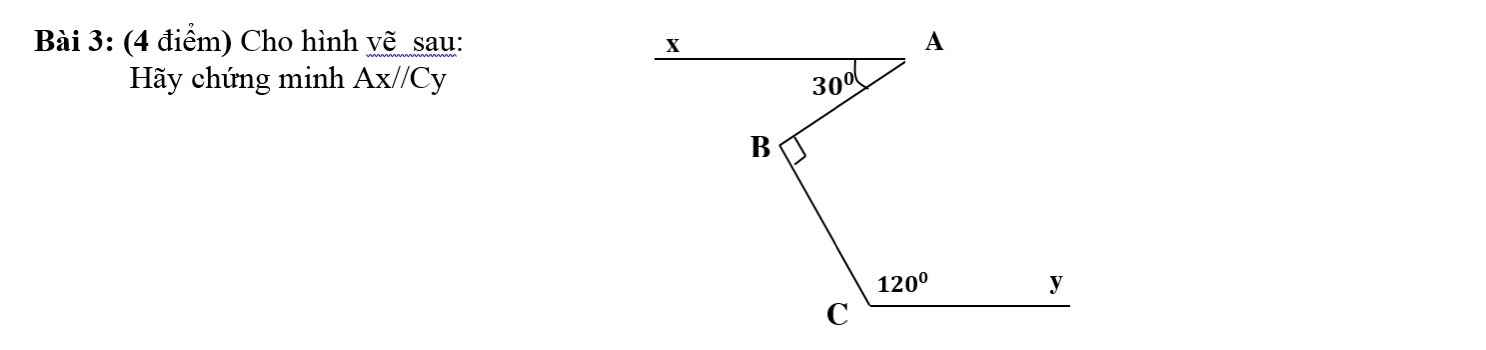
Kẻ Bz//Ax
Ta có: Ax//Bz
\(\Rightarrow\widehat{BAx}=\widehat{ABz}=30^0\)(so le trong)
\(\Rightarrow\widehat{zBC}=\widehat{ABC}-\widehat{BAx}=90^0-30^0=60^0\)
Ta có: \(\widehat{zBC}+\widehat{BCy}=60^0+120^0=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> Bz//Cy
Mà Bz//Ax
=> Ax//Cy
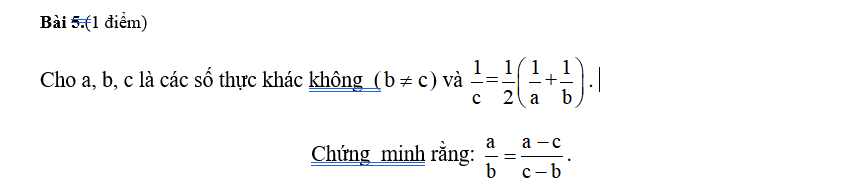
\(\left|2x+3\right|=\dfrac{1}{3}\)
⇒\(\left[{}\begin{matrix}2x+3=\dfrac{1}{3}\\2x+3=\dfrac{-1}{3}\end{matrix}\right.\)⇒\(\left[{}\begin{matrix}2x=\dfrac{1}{3}-3\\2x=\dfrac{-1}{3}-3\end{matrix}\right.\)⇒\(\left[{}\begin{matrix}2x=\dfrac{-8}{3}\\2x=\dfrac{-10}{3}\end{matrix}\right.\)
⇒\(\left[{}\begin{matrix}x=\dfrac{-4}{3}\\x=\dfrac{-5}{3}\end{matrix}\right.\)
Vậy \(x=\dfrac{-4}{3},\dfrac{-5}{3}\)