K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LD
3 tháng 4 2023
\(2x^2-3x-4=0\)
\(\Delta=3^2+4.2.4=41>0\)
⇒ Phương trình có hai nghiệm phân biệt
Theo Viét : \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{3}{2}\\x_1.x_2=-2\end{matrix}\right.\)
Lại có : \(A=\left(\dfrac{1}{x_1}\right)^2+\left(\dfrac{1}{x_2}\right)^2=\dfrac{1}{x_1^2}+\dfrac{1}{x_2^2}\)\(=\dfrac{x_1^2+x_2^2}{\left(x_1x_2\right)^2}=\dfrac{\left(x_1+x_2\right)^2-2x_1x_2}{\left(x_1x_2\right)^2}=\dfrac{\left(\dfrac{3}{2}\right)^2+4}{\left(-2\right)^2}=\dfrac{25}{16}\)
Vậy....
NT
1
LD
3 tháng 4 2023
\(x^2-2x-\sqrt{3}+1=0\)
\(\Delta'=1^2+\sqrt{3}-1=\sqrt{3}>0\)
⇒ Phương trình có hai nghiệm phân biệt
Theo Viét : \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1.x_2=1-\sqrt{3}\end{matrix}\right.\)
Ta có : \(A=x_1^2.x_2^2-2x_1x_2-x_1-x_2\)
\(=\left(x_1x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)\)
\(=\left(1-\sqrt{3}\right)^2-2\left(1-\sqrt{3}\right)-2=4-2\sqrt{3}-2+2\sqrt{3}-2=0\)
Vậy....
DK
1
20 tháng 1 2021
nhiệm là cái gì? Đề ko rõ nữa vì M = (1 - x2)x1 + (1 - x1)x2 chả có gì để cm cả :v
NT
3
Y
7 tháng 4 2023
\(x^2+1-12=0\)
Theo Vi - ét , ta có :
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=0\\x_1x_2=\dfrac{c}{a}=-11\end{matrix}\right.\)
Ta có :
\(A=x_1^2+x_2^2+x_1^2x_2+x_1x^2_2\)
\(=\left(x_1+x_2\right)^2-2x_1x_2+x_1x_2\left(x_1+x_2\right)\)
\(=0^2-2\left(-11\right)-11\left(0\right)\)
\(=22-11\)
\(=11\)
Vậy \(A=11\)
2 tháng 4 2023
x1+x2=-5/2; x1x2=-9/2
\(N=\dfrac{x_2-1+x_1-1}{\left(x_1-1\right)\left(x_2-1\right)}\)
\(=\dfrac{x_1+x_2-2}{x_1x_2-\left(x_1+x_2\right)+1}=\dfrac{\dfrac{-5}{2}-2}{-\dfrac{9}{2}+\dfrac{5}{2}+1}\)
\(=\dfrac{-9}{2}:\left(-2+1\right)=\dfrac{-9}{2}:\left(-1\right)=\dfrac{9}{2}\)
NT
2
DA
11 tháng 4 2023
xét ptr \(2x^2-x-3+0\)
△=\(\left(-1\right)^2-4.2.\left(-3\right)=25>0\)
⇒ptr có 2 ngh phân biệt \(x_1;x_2\)
Theo hệt thức viet \(x_1+x_2=\dfrac{1}{2};x_1x_2=\dfrac{-3}{2}\)
Xét A = \(x_1^2+x_2^2-x_1^2x_2^2=\left(x_1+x_2\right)^2-2x_1x_2-x_1^2x_2^2\)
=\(\left(\dfrac{1}{2}\right)^2-2\left(-\dfrac{3}{2}\right)-\left(-\dfrac{3}{2}\right)^2=\dfrac{1}{4}+3-\dfrac{9}{4}=3-2=1\)
Của cậu đây ạ, kh hiểu j thì hỏi tớ nha <3
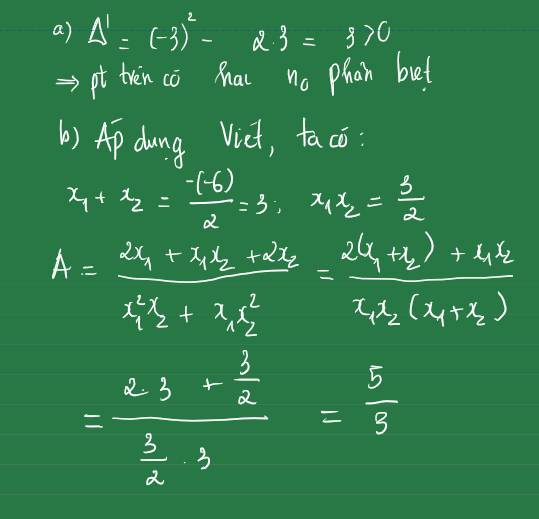
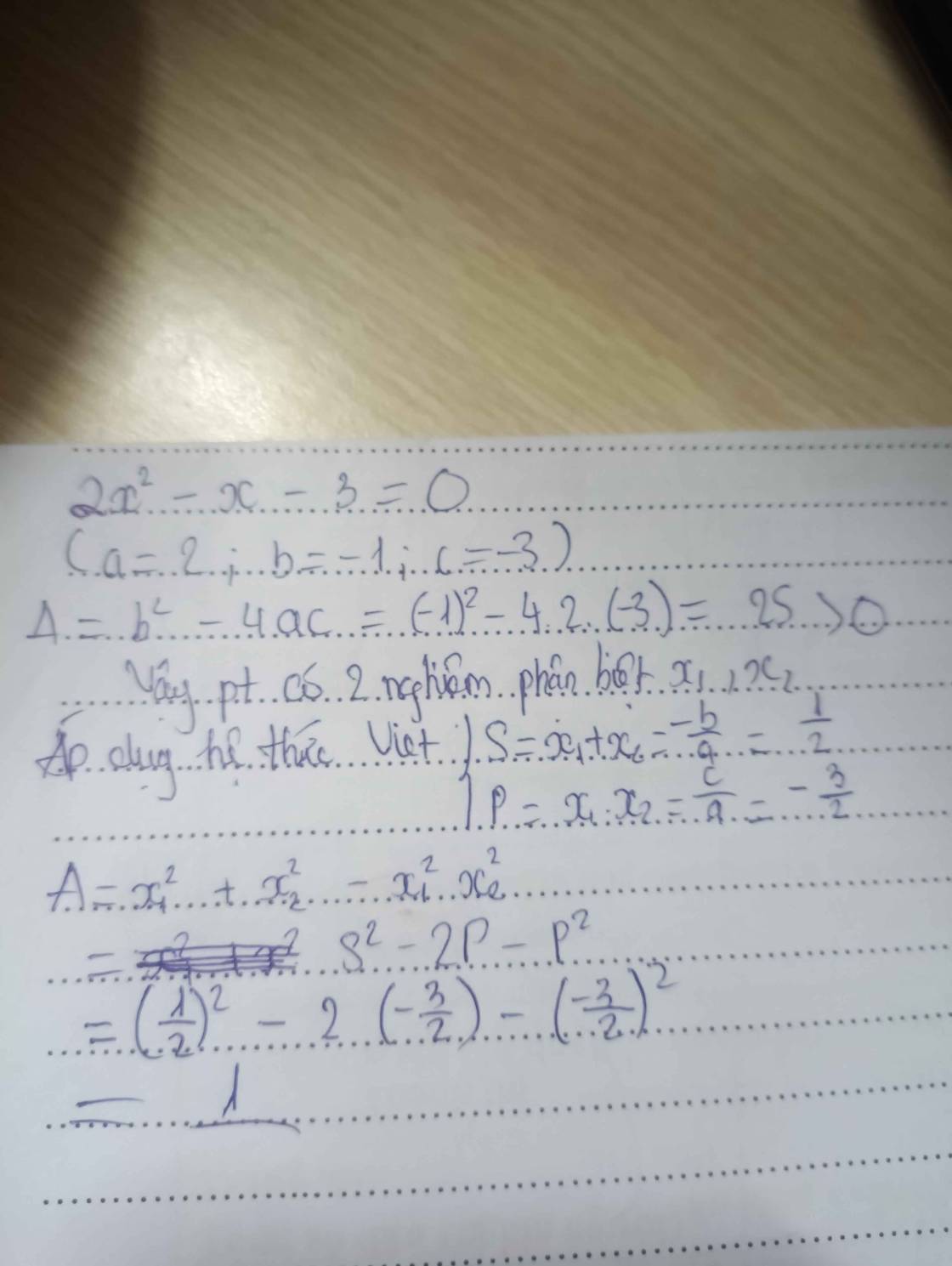
Đề khó đọc quá. Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn.