TM
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
1
11 tháng 7 2017
\(27x^3-27x^2+18x-4\)
\(=27x^3-9x^2-18x^2+6x+12x-4\)
\(=\left(27x^3-9x^2\right)-\left(18x^2-6x\right)+\left(12x-4\right)\)
\(=9x^2.\left(3x-1\right)-6x\left(3x-1\right)+4\left(3x-1\right)\)
\(=\left(3x-1\right)\left(9x^2-6x+4\right)\)
NT
3
TN
19 tháng 7 2017
\(27x^3-27x^2+18x-4\)
\(=27x^3-18x^2+12x-9x^2+6x-4\)
\(=3x\left(9x^2-6x+4\right)-\left(9x^2-6x+4\right)\)
\(=\left(3x-1\right)\left(9x^2-6x+4\right)\)
NT
19 tháng 7 2017
27x3 - 27x2 + 18x - 4
= 27x3 - 9x2 - 18x2 + 6x + 12x - 4
= 9x2 ( 3x - 1 ) - 6x ( 3x - 1 ) + 4 ( 3x - 1 )
= ( 9x2 - 6x + 4 ) ( 3x - 1 )
TL
2
KN
13 tháng 1 2020
a) \(2x^3-x^2+5x+3\)
\(=2x^3-2x^2+x^2+6x-x+3\)
\(=\left(2x^3-2x^2+6x\right)+\left(x^2-x+3\right)\)
\(=2x\left(x^2-x+3\right)+\left(x^2-x+3\right)\)
\(=\left(2x+1\right)\left(x^2-x+3\right)\)
b) \(27x^3-27x^2+18x-4\)
\(=27x^3-18x^2-9x^2+12x+6x-4\)
\(=\left(27x^3-18x^2+12x\right)-\left(9x^2-6x+4\right)\)
\(=3x\left(9x^2-6x+4\right)-\left(9x^2-6x+4\right)\)
\(=\left(3x-1\right)\left(9x^2-6x+4\right)\)
TT
1
VT
0
PT
1
3 tháng 10 2018
Nếu thế how to phân tích cái 2x^2 =)))) đề sai
2x^2 phân tích như thế nào để đặt nhân tử chung hoặc nhóm hạng tử đây???? Xem lại đề bạn ơi
KS
0
19 tháng 7 2021
a) \(x^3+9x^2+27x+27=\left(x+3\right)^3\)
b) \(3\sqrt{3x^3}+18x^2+12\sqrt{3x}+8=\left(\sqrt{3x}+2\right)^3\)
c) \(\dfrac{1}{4}-x^2=\left(\dfrac{1}{2}-x\right)\left(\dfrac{1}{2}+x\right)\)
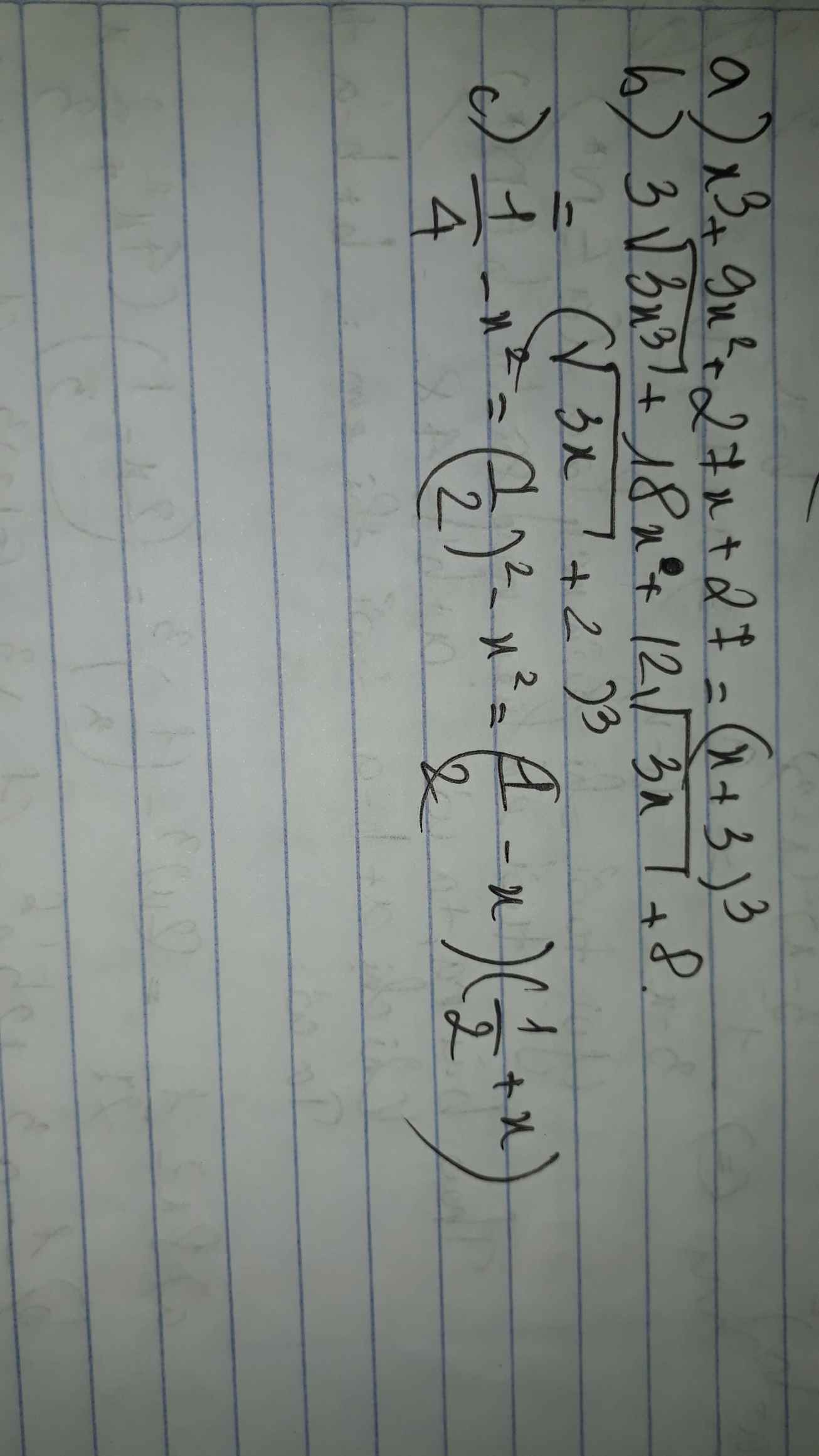
\(27x^3-27x^2+18x-4=27x^3-9x^2-18x^2+6x+12x-4\)
\(=9x^2\left(3x-1\right)-6x\left(3x-1\right)+4\left(3x-1\right)\)
\(=\left(3x-1\right)\left(9x^2-6x+4\right)\)
\(27x^3-27x^2+18x-4=27x^3-9x^2-18x^2+6x+12x-4\)
\(=9x^2\left(3x-1\right)-6x\left(3x-1\right)+4\left(3x-1\right)\)
\(=\left(3x-1\right)\left(9x^2-6x+4\right)\)