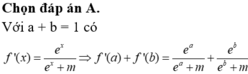Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số đơn điệu trên đoạn nên giá trị nhỏ nhất – lớn nhất sẽ đạt tại đầu mút của đoạn
Ta có f’ (x) = -x2-1< 0 với a< x< b ; suy ra hàm số y= f( x) là hàm số nghịch biến trên [ a; b].
Mà a< b nên f(a) > f( b)
Vậy m i n [ a ; b ] f ( x ) = f ( b )
Chọn C.

Theo bất đẳng thức Cauchy-Schwarz cho tích phân có:
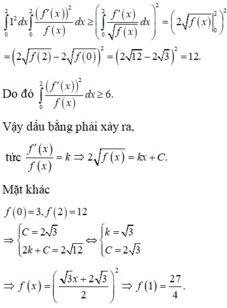
Đáp án A

\(f\left(x\right)-\left(x+1\right)f'\left(x\right)=2x.f^2\left(x\right)\)
\(\Rightarrow\dfrac{f\left(x\right)-\left(x+1\right)f'\left(x\right)}{f^2\left(x\right)}=2x\)
\(\Rightarrow\left[\dfrac{x+1}{f\left(x\right)}\right]'=2x\)
Lấy nguyên hàm 2 vế:
\(\dfrac{x+1}{f\left(x\right)}=\int2xdx=x^2+C\)
Thay \(x=1\Rightarrow\dfrac{2}{f\left(1\right)}=1+C\Rightarrow C=0\)
\(\Rightarrow f\left(x\right)=\dfrac{x+1}{x^2}\Rightarrow\int\limits^2_1\left(\dfrac{1}{x}+\dfrac{1}{x^2}\right)dx=\left(lnx-\dfrac{1}{x}\right)|^2_1=ln2+\dfrac{1}{2}\)

Cho hàm số y=f(x)y=f(x) có đạo hàm và liên tục trên [0;π2][0;π2]thoả mãn f(x)=f′(x)−2cosxf(x)=f′(x)−2cosx. Biết f(π2)=1f(π2)=1, tính giá trị f(π3)f(π3)
A. √3+1/2 B. √3−1/2 C. 1−√3/2 D. 0

Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng

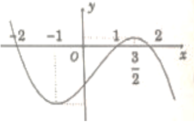
Dựa vào đồ thị hàm số ta thấy: f’(x) = 0 khi và chỉ khi x= 1; ![]()
Ta có bảng biến thiên :
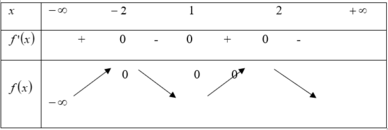
Dựa vào bảng biến thiên ta thấy f(x) < 0 với mọi x≠ ± 2
Xét hàm số y= ( f( x) ) 2 có đạo hàm y’ = 2f(x). f’ (x)
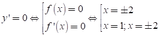
Bảng xét dấu:
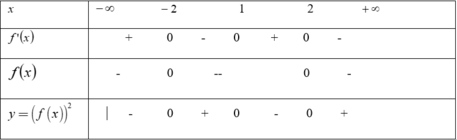
Chọn D.