Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tìm x:
a) x3 +3x2 - 10x = 0
b) x3 - 5x2 - 14x =0
c) x3 + 5x2- 24x =0
Giải giúp mình với ạ !
Mình cảm ơn !

x3+3x2-10x=0
=>x(3+3.2-10)=0
=>x=0
x3-5x2-14x=0
=>x(3-5.2-14)=0
=>x=0
x3+5x2-24x=0
=>x(3+5.2-24)=0
=>x=0
Câu a)
\(x^3+3x^2-10=0\Rightarrow x\left(x^2+3x-10\right)=0\Rightarrow x\left(x^2-2x+5x-10\right)=0\Rightarrow x\left(x\left(x-2\right)+5\left(x-2\right)\right)=0\Rightarrow x\left(x+5\right)\left(x-2\right)=0\)
\(\Rightarrow x=0;x=5;x=2\)

a) x2 - 4y2 tại x = 102 , y = \(\dfrac{1}{2}\)
= x2 - (2y)2
= (x - 2y)(x + 2y)
Thay x = 102 , y = \(\dfrac{1}{2}\) vào , ta có :
(x - 2y)(x + 2y)
= (102 - 2.\(\dfrac{1}{2}\))(102 + 2 . \(\dfrac{1}{2}\))
= 101 . 103
= 10403
b)Bạn xem lại đề b),c) có bị thiếu không, nên mình bổ sung thêm nhé :
8x3 + 12x2 + 6x + 1 tại x = \(\dfrac{29}{2}\)
= (2x)3 + 3.(2x2).1 + 3.2x.1 + 1
= (2x + 1)3
Thay x = \(\dfrac{29}{2}\) vào , ta có :
(2x + 1)3
= (2.\(\dfrac{29}{2}\) + 1)3
= (29 + 1)3
= 27000
c) x3 - 6x + 12x - 1 tại x = 102
= x3 - 3.x2.2 + 3.x.22 - 23
= (x - 2)3
Thay x = 102 vào , ta có :
(x - 2)3
= (102 - 2)3
= 1000000
Chúc bạn học tôt

a) Cách 1: Khai triển HĐT rút gọn được 3 x 2 + 6x + 7 = 0
Vì (3( x 2 + 2x + 1) + 4 < 0 với mọi x nên giải được x ∈ ∅
Cách 2. Chuyển vế đưa về ( x + 3 ) 3 = ( x - 1 ) 3 Û x + 3 = x - 1
Từ đó tìm được x ∈ ∅
b) Đặt x 2 = t với t ≥ 0 ta được t 2 + t - 2 = 0
Giải ra ta được t = 1 (TM) hoặc t = -2 (KTM)
Từ đó tìm được x = ± 1
c) Biến đổi được ![]()
d) Biến đổi về dạng x(x - 2) (x - 4) = 0. Tìm được x ∈ {0; 2; 4}

a) \(2\left(x+5\right)-x^2-5x=0\)
\(\Leftrightarrow2x+10-x^2-5x=0\)
\(\Leftrightarrow-x^2-3x+10=0\)
\(\Leftrightarrow x^2+3x-10=0\)
\(\Leftrightarrow x^2-2x+5x-10=0\)
\(\Leftrightarrow x\left(x-2\right)+5\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x+5=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2\\x=-5\end{cases}}}\)
b) \(x^3-6x^2+12x-8=0\)
\(\Leftrightarrow\left(x^3-8\right)-\left(6x^2-12x\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2+2x+4\right)-6x\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2+2x+4-6x\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2-4x+4\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-2\right)^2=0\)
\(\Leftrightarrow\left(x-2\right)^3=0\)
\(\Leftrightarrow x-2=0\Leftrightarrow x=2\)
c)\(16x^2-9\left(x+1\right)^2=0\)
\(\Leftrightarrow\left(4x\right)^2-\left[3\left(x+1\right)\right]^2=0\)
\(\Leftrightarrow\left(4x-3x-1\right)\left(4x+3x+1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(7x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\7x+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1\\x=-\frac{1}{7}\end{cases}}}\)
d) \(x^3+x=0\)
\(\Leftrightarrow x^2\left(x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x^2=0\\x+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=-1\end{cases}}}\)
e)\(x^2-2x-3=0\)
\(\Leftrightarrow x^2+x-3x-3=0\)
\(\Leftrightarrow x\left(x+1\right)-3\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\x-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-1\\x=3\end{cases}}}\)

\(a,PT\Leftrightarrow x^3-6x^2+12x-8-x^3+x+6x^2-18x-10=0\)
\(\Leftrightarrow-5x-18=0\)
\(\Leftrightarrow x=-\dfrac{18}{5}\)
Vậy ...
\(b,PT\Leftrightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1-6x^2+12x-6+10=0\)
\(\Leftrightarrow12x+6=0\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy ...
\(c,PT\Leftrightarrow\left(x+1\right)^3+3^3=0\)
\(\Leftrightarrow\left(x+1+3\right)\left(x^2+2x+1-3x-3+9\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x^2-x+7\right)=0\)
Thấy : \(x^2-\dfrac{2.x.1}{2}+\dfrac{1}{4}+\dfrac{27}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{27}{4}\ge\dfrac{27}{4}>0\)
\(\Rightarrow x+4=0\)
\(\Leftrightarrow x=-4\)
Vậy ...
\(d,PT\Leftrightarrow\left(x-2\right)^3+1^3=0\)
\(\Leftrightarrow\left(x-2+1\right)\left(x^2-4x+4-x+2+1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-5x+7\right)=0\)
Thấy : \(x^2-5x+7=x^2-\dfrac{5.x.2}{2}+\dfrac{25}{4}+\dfrac{3}{4}=\left(x-\dfrac{5}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\)
\(\Rightarrow x-1=0\)
\(\Leftrightarrow x=1\)
Vậy ...

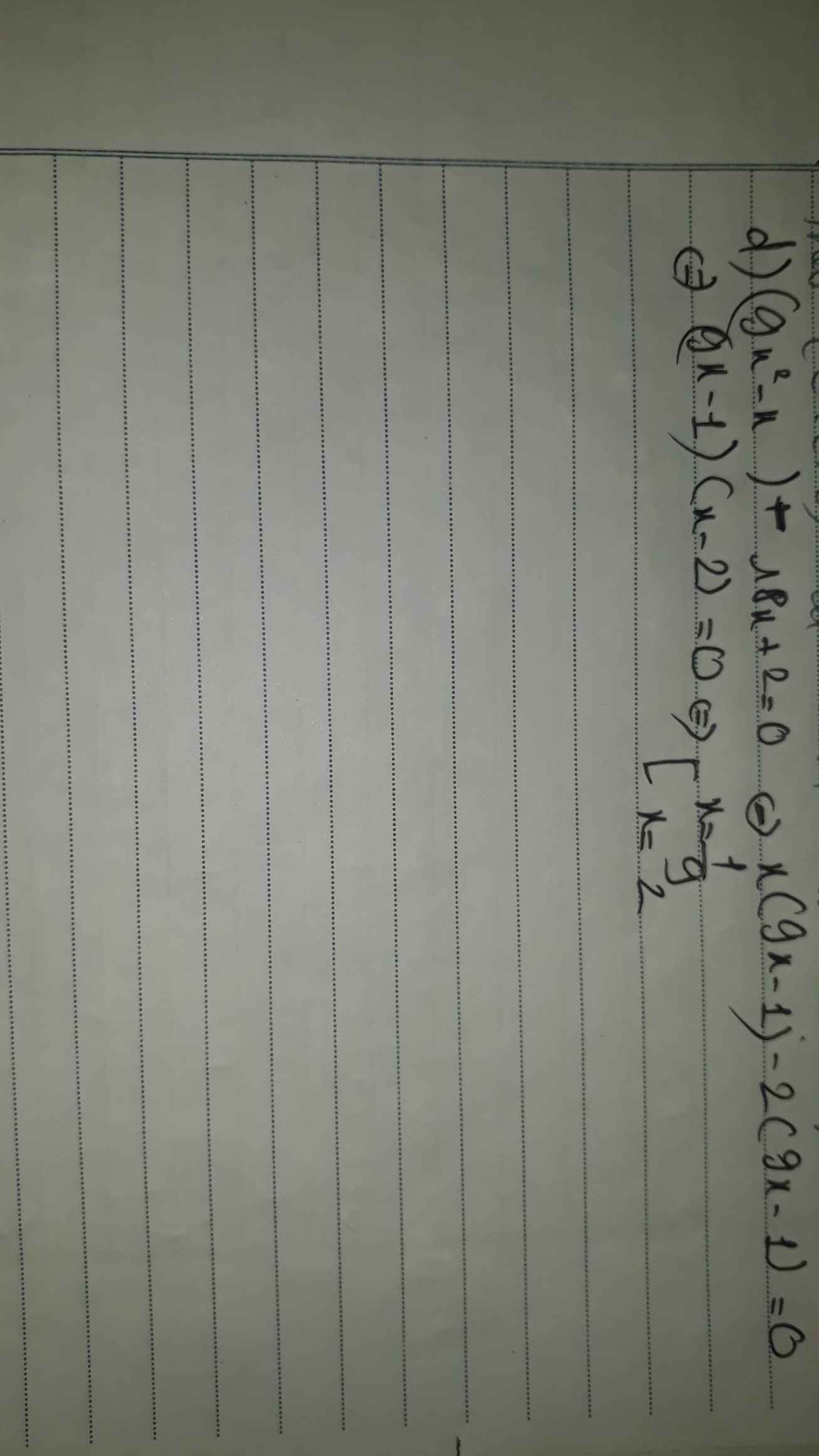
a) x^3 - 6x^2 + 12x -8 = 0
x^3 - 3.x^2 .2 + 3.x.2^2 - 2^3 = 0
=> ( x-2) = 0
=> x-2=0 <=> x=2
b) 8x^3 - 12x^2 + 6x -1 = 0
(2x)^3 - 3.(2x)^2.1 + 3.2x.1 -1^3 = 0
=> ( 2x - 1 ) = 0
=> 2x-1 = 0 <=> 2x = 1
x = 1/2