Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x, y (ngày) lần lượt là thời gian mà người thứ nhất và người thứ hai làm riêng xong công việc. Điều kiện: x > 4, y > 4.
Như vậy, trong 1 ngày người thứ nhất làm được 1/x (công việc), người thứ hai làm được 1/y (công việc).
Trong 1 ngày, cả hai người làm được 1 : 4 = 1/4 (công việc)
Ta có phương trình: 1/x + 1/y = 1/4
Nếu người thứ nhất làm một mình trong 9 ngày rồi người thứ hai đến cùng làm tiếp trong 1 ngày nữa thì xong việc, ta có phương trình:
10/x + 1/y = 1
Ta có hệ phương trình:
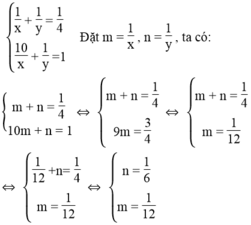
Ta có: 1/x = 1/12 ⇔ x = 12
1/y = 1/6 ⇔ y = 6
Giá trị của x và y thỏa điều kiện bài toán.
Vậy người thứ nhất làm một mình xong công việc trong 12 ngày, người thứ hai làm một mình xong công việc trong 6 ngày.
Sao lại có số 10 vậy bạn , người thứ nhất làm xong 9 ngày mà có số 10 nên mik ko hiểu lắm ??

gọi thời gian người thứ nhất làm xong công việc là x(x>0)
thời gian người thứ hai làm xong công việc là y(y>0)
1 ngày hai người làm chung sẽ làm được \(\frac{1}{x}+\frac{1}{y}\) (công việc)
ta có hệ phương trình \(\frac{1}{x}+\frac{1}{y}=\frac{1}{4}\)
\(\frac{10}{x}+\frac{1}{y}=1\)
giải hệ phương trình trên ta sẽ tìm được
Dãy số có 2 chữ số chia hết cho 3 là:[12,15,....,99]
Khoảng cách của từng số hạng là 3
Số số hạng là: (99-12):3+1=30(số)
Vậy có 30 số có 2 chữ số chia hết cho 3

Lời giải:
Giả sử nếu làm 1 mình thì người 1 và người 2 lần lượt hoàn thành công việc trong $a$ và $b$ giờ
Trong 1 giờ: Người 1 làm $\frac{1}{a}$ công việc, người 2 làm $\frac{1}{b}$ công việc.
Theo bài ra ta có:
\(\left\{\begin{matrix} \frac{18}{a}+\frac{18}{b}=1\\ \frac{15+9}{a}+\frac{9}{b}=1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \frac{18}{a}+\frac{18}{b}=1\\ \frac{24}{a}+\frac{9}{b}=1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \frac{1}{a}=\frac{1}{30}\\ \frac{1}{b}=\frac{1}{45}\end{matrix}\right.\)
Vậy người thứ 2 làm một mình trong 45 giờ thì hoàn thành.

Gọi x là số ngày của người 1 làm 1 mình xong việc
y là số ngày của người 2 làm 1 mình xong việc
ĐK: x;y > 0
Số việc người 1 làm trong 1h là \(\frac{1}{x}\)
Số việc người 2 làm trong 1h là \(\frac{1}{y}\)
Theo đề bài ta có hệ phương trình:
\(\hept{\begin{cases}4\left(\frac{1}{x}+\frac{1}{y}\right)=1\\10.\frac{1}{x}+\frac{1}{y}=1\end{cases}}\)
Từ đó bạn giải hệ và kết luận.

Làm lại qua đây vậy:
Gọi số ngày người thứ nhất làm một mình xong việc là x
số ngày người thứ hai làm một mình xong việc là y
ĐK: x;y > 0
Số việc người thứ nhất làm trong 1h là: \(\frac{1}{x}\)
Số việc người thứ hai làm trong 1h là: \(\frac{1}{y}\)
Theo đề bài ta có hệ phương trình:
\(\hept{\begin{cases}4\left(\frac{1}{x}+\frac{1}{y}\right)=1\\10.\frac{1}{x}+\frac{1}{y}=1\end{cases}}\)
Từ đây bạn giải tiếp & kết luận. Không hiểu hỏi nha hiccc
