Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

P = 7 + 72 + 73 + ... + 72016
=> P = 7( 1 + 7 + 72 + 73) + ... + 72013( 1 + 7 + 72 + 73)
=> P = 7( 1 + 7 + 49 + 343) + ... + 72013( 1 + 7 + 49 + 343)
=> P = 7 . 400 + ... + 72013 . 400
=> P = (7 + ... + 72013) . 400
=> P = (7 + ... + 72013) . 202 (đpcm)

Đáp án D
Chọn ngẫu nhiên 2 người có Ω = C 10 2 cách
Gọi A là biến cố: 2 người được chọn đều là nữ
Ta có Ω A = C 3 2 Do đó sác xuất cần tìm là P A = C 3 2 C 10 2 = 1 15

Chọn B.
Phương pháp
Tính xác suất theo định nghĩa P A = n A n Ω với n(A) là số phần tử của biến cố A, n Ω là số phấn tử
của không gian mẫu.
Cách giải:
Số phần tử của không gian mẫu n Ω = C 20 2
Gọi A là biến cố “Hai người được chọn có it nhất một nữ” thì A là biến cố hai người được chọn không có nữ nào, tức là ta chọn 2 người trong số 7 nam.
Khi đó n A = C 7 2 ⇒ n A = C 10 2 - C 7 2
Xác suất để hai người được chọn có it nhất một nữ là P = C 10 2 - C 7 2 C 10 2 = 8 15

Thời gian người thứ hai đi hết quãng đường AB là: \(1:\frac{1}{9}=9\) (giờ).
Từ 7 giờ đến 9 giờ, người thứ nhất đi được \(\frac{1}{11}\cdot2=\frac{2}{11}\) quãng đường AB, tức người thứ nhất đi trước người thứ 2 là \(\frac{2}{11}\) quãng đường AB.
Vận tốc người thứ hai hơn người thứ nhất là: \(\frac{1}{9}-\frac{1}{11}=\frac{2}{99}\) (quãng đường AB)
Thời gian người thứ hai đuổi kịp người thứ nhất kể từ lúc người thứ hai xuất phát là: \(\frac{2}{11}:\frac{2}{99}=9\) (giờ).
Như vậy hai người gặp nhau lần đầu tại B.
Vậy trong suốt quãng đường AB người thứ hai không vượt được người thứ nhất.

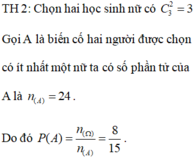

~
Tuyệt vời quá!
Hoc24 cảm ơn Lan Anh nhiều! Nếu bạn gửi thêm câu trả lời nữa thì được câu trắc nghiệm hoàn chỉnh và Hoc24 sẽ sử dụng làm câu trắc nghiệm cho chủ đề này đồng thời sẽ tặng bạn 3GP!