Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Cách 1.
Ta có 2xy + 3z + 6y + xz = (2xy + xz) + (3z + 6y)
= x(2 y + z)+3(z + 2 y) = (z + 2y)(x + 3).
Cách 2.
Ta có 2xy + 3z + 6y + xz = (2x1/ + 6y) + (3z + xz)
= 2y(x + 3) + z(3 + x) = (z + 2y)(x + 3).
b) Biến đổi được a 4 - 9 rt 3 + a 2 -9a = (a- 9)a( a 2 +1).
c) Biến đổi được 3 x 2 + 5y - 3xy + (-5x) = (x - y)(3x - 5).
d) Biến đổi được x 2 - (a + b)x + ab = (x- a)(x - b).
e) Ta có 4 x 2 - 4xy + y 2 – 9 t 2 = ( 2 x - y ) 2 - ( 3 t ) 2
= (2x - y - 3t )(2x - y + 31).
g) Ta có x 3 - 3 x 2 y + 3 xy 2 - y 3 - z 3
= ( x - y ) 3 - z 3 = (x - y - z)( x 2 + y 2 + z 2 - 2xy + xz - yz).
h) Ta có x 2 - y 2 + 8x + 6y+ 7 = ( x 2 +8x + 16) - ( y 2 - 6y+ 9)
= ( x + 4 ) 2 - ( y - 3 ) 2 =(x-y + 7)(x + y + l).

a) \(6x-6y=6\left(x-y\right)\)
b)\(2xy+3x+6y+xz\)
\(=\left(2xy+xz\right)+\left(6y+3z\right)\)
\(=x\left(2y+z\right)+3\left(2y+z\right)\)
\(=\left(2y+z\right)\left(x+3\right)\)
c)\(x^2+6x+9-y^2\)
\(=\left(x^2+6x+9\right)-y^2\)
\(=\left(x+3\right)^2-y^2\)
\(=\left(x-y+3\right)\left(x+y+3\right)\)
d) \(9x-x^3\)
\(=x\left(9-x^2\right)\)
\(=x\left(3-x\right)\left(3+x\right)\)
e)\(x^2-xy+x-y\)
\(=\left(x^2-xy\right)+\left(x-y\right)\)
\(=x\left(x-y\right)+\left(x-y\right)\)
\(=\left(x-y\right)\left(x+1\right)\)
a, 6x - 6y = 6( x-y )
b, 2xy + 3z + 6y + xz
= ( 2xy + 6y ) + ( 3z + xz )
= 2y( x + 3 ) + z ( 3 + x )
= 2y( 3 + x ) + z ( 3 + x )
= ( 3 + x ) ( 2y + z )
c, x2 + 6x + 9 - y2 = ( x2 + 6x + 9 ) - y2
= ( x + 3 )2 - y2
= ( x + 3 - y ) ( x + 3 + y )
d , 9x - x3 = x ( 9 - x2 )
= x ( 3 - x ) ( 3 + x )
e, x2 - xy + x - y =( x 2 - xy ) + ( x - y )
= x ( x - y ) + ( x - y )
= ( x - y ) ( x + 1 )

e: \(x^2+6x+9-y^2\)
\(=\left(x+3\right)^2-y^2\)
\(=\left(x+3-y\right)\left(x+3+y\right)\)
f: \(x^2-2x+7x-14\)
\(=x\left(x-2\right)+7\left(x-2\right)\)
=(x-2)(x+7)
h: \(5x^2-10xy+5y^2-20\)
\(=5\left(x^2-2xy+y^2-4\right)\)
\(=5\left(x-y-2\right)\left(x-y+2\right)\)

a: \(3x^4-6x^3+2x^2=x^2\left(3x^2-6x+2\right)\)
b: \(x^3y+12x^2y+36xy=xy\left(x^2+12x+36\right)=xy\left(x+6\right)^2\)
c: \(x^3y-9xy^3=xy\left(x^2-9y^2\right)=xy\left(x-3y\right)\left(x+3y\right)\)
d: \(x^2y^2-2xy^2+y^2=y^2\left(x-1\right)^2\)

a) x2 - 6x +9 = (x-3)2
b) x2 - 64 = (x-8)(x+8)
c) 2xy+3z+6y+xz = (2xy+xz)=(3z+6y)= x(2y+z) + 3(2y+z)=(2y+z)(x+3)
d) 5x2+5xy-x-y = 5x(x+y)-(x+y) = (x+y)(5x-1)
e) x2 - xy+ x-y = x(x-y)+(x-y) = (x-y)(x+1)
CHÚC BN HỌC TỐT

\(M=x^2-5x+xy-5y=\left(x+y\right)\left(x-5\right)\)
\(N=x^2-3x-2xy+y^2+3y=\left(x-y\right)\left(x-y-3\right)\)\(K=2xy+3z+6y+xz=\left(x+3\right)\left(2y+z\right)\)
M= x2-5x+xy-5y= x(x-5)+y(x-5)=(x-5)(x+y)
N= x2-3x-2xy+y2+3y=(x-y)2-3(x-y)=(x-y)(x-y-3)
K= 2xy+3z+6y+xz=2y(x+3)+z(x+3)=(x+3)(2y+z)

a.
\(1-4x^2=\left(1-2x\right)\left(1+2x\right)\)
b.
\(8-27x^3=\left(2\right)^3-\left(3x\right)^3=\left(2-3x\right)\left(4+6x+9x^2\right)\)
c.
\(27+27x+9x^2+x^3=x^3+3.x^2.3+3.3^2.x+3^3\)
\(=\left(x+3\right)^3\)
d.
\(2x^3+4x^2+2x=2x\left(x^2+2x+1\right)=2x\left(x+1\right)^2\)
e.
\(x^2-y^2-5x+5y=\left(x-y\right)\left(x+y\right)-5\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y-5\right)\)
f.
\(x^2-6x+9-y^2=\left(x-3\right)^2-y^2=\left(x-3-y\right)\left(x-3+y\right)\)

c) \(5x^2+3y+15x+xy=5x\left(x+3\right)+y\left(x+3\right)=\left(x+3\right)\left(5x+y\right)\)
d) \(x^2+6x+9-y^2=\left(x+3\right)^2-y^2=\left(x+3-y\right)\left(x+3+y\right)\)
e) \(x^2-y^2+2x+1=\left(x^2+2x+1\right)-y^2=\left(x+1\right)^2-y^2=\left(x+1-y\right)\left(x+1+y\right)\)
f) \(x^2-2xy-9+y^2=\left(x^2-2xy+y^2\right)-9=\left(x-y\right)^2-3^2=\left(x-y-3\right)\left(x-y+3\right)\)
c: \(5x^2+15x+3y+xy\)
\(=5x\left(x+3\right)+y\left(x+3\right)\)
\(=\left(x+3\right)\left(5x+y\right)\)
d: \(x^2+6x+9-y^2\)
\(=\left(x+3\right)^2-y^2\)
\(=\left(x+3-y\right)\left(x+3+y\right)\)
e: \(x^2+2x+1-y^2\)
\(=\left(x+1\right)^2-y^2\)
\(=\left(x+1-y\right)\left(x+1+y\right)\)
f: \(x^2-2xy+y^2-9\)
\(=\left(x-y\right)^2-9\)
\(=\left(x-y-3\right)\left(x-y+3\right)\)
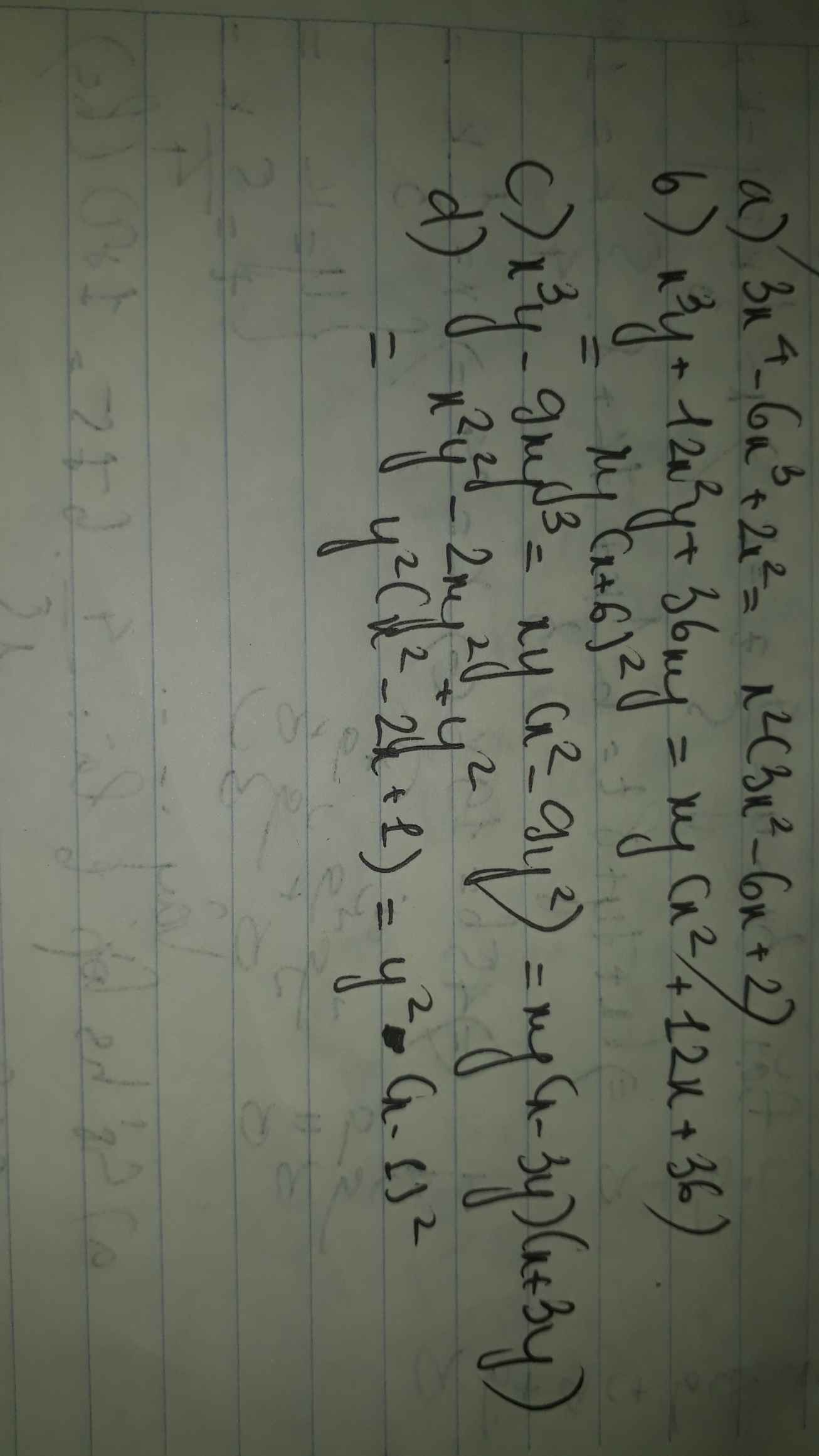
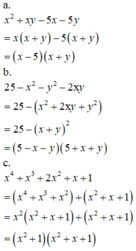
a. \(x^2+6x-y^2+9=\left(x+3\right)^2-y^2=\left(x+3-y\right)\left(x+3+y\right)\)
b. \(2x^2-4x+2=2\left(x^2-2x+1\right)=2\left(x-1\right)^2\)
c. \(2xy+3z+6y+xz=2xy+6y+3z+xz=2y\left(x+3\right)+z\left(3+x\right)=\left(2y+z\right)\left(x+3\right)\)