Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) A = 2n +1 => A là số lẻ \(\Rightarrow⋮̸\)( không chia hết ) 2
b) A có thể chia hết cho 5 , A có thể không chia hết cho 5

a: Ta có: \(3n+2⋮n-1\)
\(\Leftrightarrow n-1\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{2;0;6;-4\right\}\)

Ta có:5n+6 chia hết cho 3n-2 =>3(5n+6) chia hết cho 3n-2 hay15n+18 chia hết cho 3n-2(1)
3n-2=5(3n-2)=15n-10(2)
Từ (1) và (2) =>[(15n+8)-(15n-10)] chia hết cho 3n-2
18 chia hết cho 3n-2
(3n-2) có thể bằng :9,2,3,6,1,18
Nếu 3n-2=9 thì n=(9+2):3 loại vì 11 không chia hết cho 3
Nếu 3n-2=2 thì n=(2+2):3 loại vì 4 không chia hết cho 3
Nếu 3n-2=3 thì n=(3+2):3 loại vì 5 không chia hết cho 3
Nếu 3n-2=6 thì n=(6+2):3 loại vì 8 không chia hết cho 3
Nếu 3n-2=1 thì n=(1+2):3 chọn vì 3 chia hết cho 3
Nếu 3n-2=18 thì n=(18+2):3 loại vì 2 không chia hết cho 3
Vậy n=1
n2+4 chia hết cho n-2
Ta có:n2+4=n.n+4.n=n(4+n)
n-1=n.n-n.1=n(n-1)
n2+4 chia hết cho n-1 hay n(4+n)chia hết cho n(n-1)
=4+n chia hết cho n-1
=> n chỉ có thể là 2

a, n-4 chia hết cho n-1
Vì n-1 \(_⋮\)n-1 nên 3\(_⋮\)n-1
\(\Rightarrow\)n-1 \(_{\in}\)Ư(3)
Ư(3)={1;-1;3;-3}| n-1 | -1 | -3 | 1 | 3 |
| n | 0 | -2 | 2 | 4 |
Vậy n\(_{\in}\){0;2;-2;4}
b, n-2 chia hết cho n+1
Ta có: n-2=n+1-3
\(\Rightarrow\)n-1+3\(_⋮\)n+1
\(\Rightarrow\)3\(_⋮\)n+1
\(\Rightarrow\)n+1\(_{\in}\)Ư(3)
Ư(3)={1;-1;3;-3}
| n+1 | 1 | -1 | 3 | -3 |
| n | 0 | -2 | 2 | -4 |
Vậy n\(_{\in}\){0;-2;2;-4}

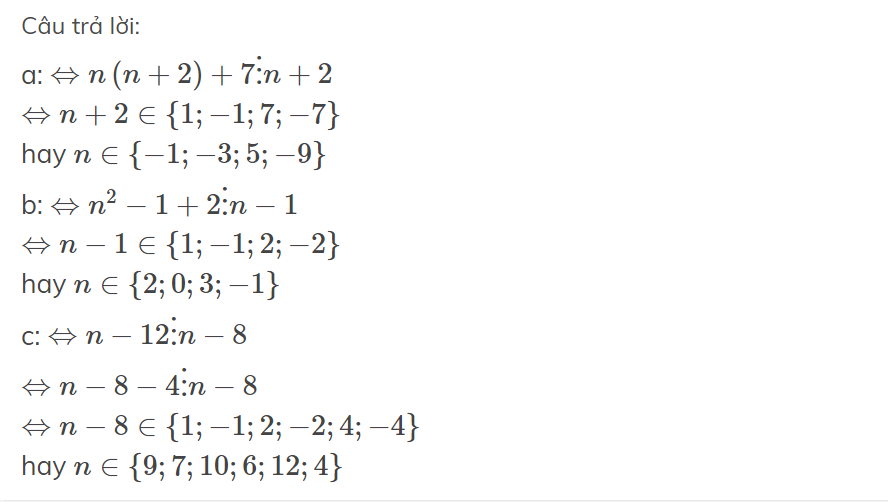
n2 + 3n - 13 chia hết cho n + 3
=> n(n + 3) - 13 chia hết cho n + 3
=> 13 chia hết cho n + 3
=> n + 3 thuộc Ư(13) = {1;-1;13;-13}
Vậy n thuộc {-2;-4;10;-16}
n2 + 3 chia hết cho n - 1
=> n2 - 1 + 4 chia hết cho n - 1
=> (n - 1)(n + 1) + 4 chia hết cho n - 1
=> 4 chia hết cho n - 1
=> n - 1 thuộc Ư(4) = {1;-1;2;-2;4;-4}
Vậy n thuộc {2;0;3;-1;5;-3}