Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(P=\dfrac{5a+10b+15c}{4}+\left(\dfrac{3}{a}+\dfrac{3a}{4}\right)+\left(\dfrac{9}{2b}+\dfrac{b}{2}\right)+\left(\dfrac{4}{c}+\dfrac{c}{4}\right)\)
\(\ge\dfrac{5\left(a+2b+3c\right)}{4}+2\sqrt{\dfrac{3}{a}.\dfrac{3a}{4}}+2\sqrt{\dfrac{9}{2b}.\dfrac{b}{2}}+2\sqrt{\dfrac{4}{c}.\dfrac{c}{4}}\)
\(\Leftrightarrow P\ge\dfrac{5.20}{4}+3+3+2=33\)
Dấu "=" xảy ra khi a=2;b=3;c=4
Vậy \(P_{min}=33\)

3a)\(\left\{{}\begin{matrix}\dfrac{1}{x-2}+\dfrac{1}{2y-1}=2\\\dfrac{2}{x-2}-\dfrac{3}{2y-1}=1\end{matrix}\right.\) (ĐK: x≠2;y≠\(\dfrac{1}{2}\))
Đặt \(\dfrac{1}{x-2}=a;\dfrac{1}{2y-1}=b\) (ĐK: a>0; b>0)
Hệ phương trình đã cho trở thành
\(\left\{{}\begin{matrix}a+b=2\\2a-3b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2-b\\2\left(2-b\right)-3b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2-b\\4-2b-3b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2-b\\b=\dfrac{3}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{7}{5}\left(TM\text{Đ}K\right)\\b=\dfrac{3}{5}\left(TM\text{Đ}K\right)\end{matrix}\right.\) Khi đó \(\left\{{}\begin{matrix}\dfrac{1}{x-2}=\dfrac{7}{5}\\\dfrac{1}{2y-1}=\dfrac{3}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7\left(x-2\right)=5\\3\left(2y-1\right)=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7x-14=5\\6y-3=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{19}{7}\left(TM\text{Đ}K\right)\\y=\dfrac{4}{3}\left(TM\text{Đ}K\right)\end{matrix}\right.\) Vậy hệ phương trình đã cho có nghiệm duy nhất (x;y)=\(\left(\dfrac{19}{7};\dfrac{4}{3}\right)\)
b) Bạn làm tương tự như câu a kết quả là (x;y)=\(\left(\dfrac{12}{5};\dfrac{-14}{5}\right)\)
c)\(\left\{{}\begin{matrix}3\sqrt{x-1}+2\sqrt{y}=13\\2\sqrt{x-1}-\sqrt{y}=4\end{matrix}\right.\)(ĐK: x≥1;y≥0)
\(\Leftrightarrow\left\{{}\begin{matrix}3\sqrt{x-1}+2\sqrt{y}=13\\\sqrt{y}=2\sqrt{x-1}-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3\sqrt{x-1}+4\sqrt{x-1}=13\\\sqrt{y}=2\sqrt{x-1}-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7\sqrt{x-1}=13\\\sqrt{y}=2\sqrt{x-1}-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}49\left(x-1\right)=169\\\sqrt{y}=2\sqrt{x-1}-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}49x-49=169\\\sqrt{y}=2\sqrt{x-1}-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{218}{49}\\y=\dfrac{4}{49}\end{matrix}\right.\left(TM\text{Đ}K\right)\)
Bài 4:
Theo đề, ta có hệ:
\(\left\{{}\begin{matrix}3\left(3a-2\right)-2\left(2b+1\right)=30\\3\left(a+2\right)+2\left(3b-1\right)=-20\end{matrix}\right.\)
=>9a-6-4b-2=30 và 3a+6+6b-2=-20
=>9a-4b=38 và 3a+6b=-20+2-6=-24
=>a=2; b=-5

\(\Leftrightarrow\left\{{}\begin{matrix}a+b=\dfrac{5}{6}\\\dfrac{6a+14b}{9}=\dfrac{9}{9}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=\dfrac{5}{6}\\6a+14b=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{5}{6}-b\\6\left(\dfrac{5}{6}-b\right)+14b=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{5}{6}-b\\5-6b+14b=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{5}{6}-b\\8b=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{5}{6}-\dfrac{1}{2}=\dfrac{1}{3}\\b=\dfrac{1}{2}\end{matrix}\right.\)
\(\left\{{}\begin{matrix}a+b=\dfrac{5}{6}\\\dfrac{2a}{3}+\dfrac{14b}{9}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{14a}{9}+\dfrac{14b}{9}=\dfrac{35}{27}\\\dfrac{2a}{3}+\dfrac{14b}{9}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{8}{9}a=\dfrac{8}{27}\\\dfrac{2a}{3}+\dfrac{14b}{9}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{3}\\\dfrac{2a}{3}+\dfrac{14b}{9}=1\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{2.\dfrac{1}{3}}{3}+\dfrac{14b}{9}=1\)
\(\Leftrightarrow\dfrac{14b}{9}=1-\dfrac{2}{9}=\dfrac{7}{9}\)
\(\Leftrightarrow b=\dfrac{7}{9}:\dfrac{14}{9}=\dfrac{1}{2}\)
Vậy ...

\(Q=\dfrac{2002}{a}+\dfrac{2017}{b}+2996a-5501b=\left(\dfrac{2002}{a}+8008a\right)+\left(\dfrac{2017}{b}+2017b\right)-\left(5012a+7518b\right)\)
\(=\left(\dfrac{2002}{a}+8008a\right)+\left(\dfrac{2017}{b}+2017b\right)-2506\left(2a+3b\right)\)
Áp dụng bất đẳng thức Cosi cho 2 số dương:
\(\left\{{}\begin{matrix}\dfrac{2002}{a}+8008\ge2\sqrt{\dfrac{2002}{a}.8008}=8008\\\dfrac{2017}{b}+2017b\ge2\sqrt{\dfrac{2017}{b}.2017b}=4034\end{matrix}\right.\)
Ta có: \(2a+3b=4\Rightarrow-\left(2a+3b\right)=-4\Leftrightarrow-2506\left(2a+3b\right)=-10024\)
\(\Rightarrow Q\ge8008+4034-10024=2018\)
\(ĐTXR\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=1\end{matrix}\right.\)

a: \(\Leftrightarrow\left\{{}\begin{matrix}\left(x+2\right)\left(y+3\right)-xy=100\\xy-\left(x-2\right)\left(y-2\right)=64\end{matrix}\right.\)
=>xy+3x+2y+6-xy=100 và xy-xy+2x+2y-4=64
=>3x+2y=94 và 2x+2y=68
=>x=26 và x+y=34
=>x=26 và y=8
b: \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3x+3+2}{x+1}-\dfrac{2}{y+4}=4\\\dfrac{2x+2-2}{x+1}-\dfrac{5y+20-11}{y+4}=9\end{matrix}\right.\)
=>\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x+1}-\dfrac{2}{y+4}=4-3=1\\\dfrac{-2}{x+1}+\dfrac{11}{y+4}=9+5-2=12\end{matrix}\right.\)
=>x+1=18/35; y+4=9/13
=>x=-17/35; y=-43/18

\(a) \begin{cases}x=y+4\\2x+3=0\end{cases}\Leftrightarrow\begin{cases}x = y + 4\\2x = -3\end{cases}\Leftrightarrow\begin{cases}\dfrac{-3}{2} = y + 4\\x = \dfrac{-3}{2}\end{cases}\Leftrightarrow\begin{cases}y = \dfrac{-11}{2}\\x = \dfrac{-3}{2}\end{cases}\\b) \begin{cases}2x + y = 7\\3y - x = 7\end{cases}\Leftrightarrow\begin{cases}2x + y = 7\\6y - 2x = 14\end{cases}\Leftrightarrow\begin{cases}2x + y = 7\\7y = 21\end{cases}\Leftrightarrow\begin{cases}2x + 3 = 7\\y = 3\end{cases}\Leftrightarrow\begin{cases}x=2\\y=3\end{cases}\\ c) \begin{cases} 5x + y = 3 \\ -x - \dfrac{1}{5}y=\dfrac{-3}{5} \end{cases} \Leftrightarrow \begin{cases} 5x + y = 3 \\ 5x + y = 3 \end{cases} (luôn\ đúng) \Leftrightarrow Phương\ trình\ vô\ số\ nghiệm \\d) \begin{cases} 3x - 5y = -18 \\ x - 5 = 2y \end{cases} \Leftrightarrow \begin{cases} 3x - 5y = -18 \\ 3x - 6y = 15 \end{cases} \Leftrightarrow \begin{cases} x - 5 = 2.(-33)\\ y = -13 \end{cases} \Leftrightarrow \begin{cases}x = -61\\y=-33 \end{cases} \)

Tất cả các hpt này đều giải bằng PP đặt ẩn phụ
a) \(\begin{cases}2\left(x+y\right)+3\left(x-y\right)=4\\\left(x+y\right)+2\left(x-y\right)=5\end{cases}\)
Đặt \(x+y=a\) ; \(x-y=b\) ta được:
\(\begin{cases}2a+3b=4\\a+2b=5\end{cases}\) \(\Leftrightarrow\) \(\begin{cases}2a+3b=4\\2a+4b=10\end{cases}\)\(\Leftrightarrow\) \(\begin{cases}-b=-6\\2a+4b=10\end{cases}\)
\(\Leftrightarrow\) \(\begin{cases}b=6\\2a+4.6=10\end{cases}\) \(\Leftrightarrow\) \(\begin{cases}a=-7\\b=6\end{cases}\) \(\Leftrightarrow\) \(\begin{cases}x+y=6-7\\x-y=6-7\end{cases}\)
\(\Leftrightarrow\) \(\begin{cases}x-7=-1\\6-y=-1\end{cases}\) \(\Leftrightarrow\) \(\begin{cases}x=6\\y=-7\end{cases}\)
Lúc khác mình làm tiếp mấy câu kia
Tiếp nào!
b) \(\begin{cases}\dfrac{3}{x}-\dfrac{4}{y}=2\\\dfrac{4}{x}-\dfrac{5}{y}=3\end{cases}\) Đặt \(\dfrac{1}{x}=a\) ; \(\dfrac{1}{y}=b\) ta được:
\(\begin{cases}3a-4b=2\\4a-5b=3\end{cases}\) \(\Leftrightarrow\) \(\begin{cases}12a-16b=8\\12a-15b=9\end{cases}\) \(\Leftrightarrow\) \(\begin{cases}-1b=-1\\12a-15b=9\end{cases}\)
\(\Leftrightarrow\) \(\begin{cases}b=1\\a=2\end{cases}\)\(\Leftrightarrow\) \(\begin{cases}a=2\\b=1\end{cases}\) \(\Leftrightarrow\) \(\begin{cases}\dfrac{1}{a}=2\\\dfrac{1}{b}=1\end{cases}\) \(\Leftrightarrow\) \(\begin{cases}a=\dfrac{1}{2}\\b=1\end{cases}\)
c) Làm tương tự thay \(\dfrac{1}{2x-y}=a\) ; \(\dfrac{1}{x+y}=b\)

Xí câu BĐT:
ta cần chứng minh \(\dfrac{a^2}{b^2c}+\dfrac{b^2}{c^2a}+\dfrac{c^2}{a^2b}\ge\dfrac{ab+bc+ca}{abc}\)
\(\Leftrightarrow\dfrac{a^3}{b}+\dfrac{b^3}{c}+\dfrac{c^3}{a}\ge ab+bc+ca\)
Áp dụng BĐT cauchy:
\(\dfrac{a^3}{b}+ab\ge2\sqrt{\dfrac{a^3}{b}.ab}=2a^2\)
tương tự ta có:\(\dfrac{b^3}{c}+bc\ge2b^2;\dfrac{c^3}{a}+ac\ge2c^2\)
cả 2 vế các BĐT đều dương,cộng vế với vế ta có:
\(\dfrac{a^3}{b}+\dfrac{b^3}{c}+\dfrac{c^3}{a}+ab+bc+ca\ge2a^2+2b^2+2c^2\)
\(\Leftrightarrow\dfrac{a^3}{b}+\dfrac{b^3}{c}+\dfrac{c^3}{a}\ge2\left(a^2+b^2+c^2\right)-\left(ab+bc+ca\right)\)
mà a2+b2+c2\(\ge ab+bc+ca\) ( chứng minh đầy đủ nhá)
do đó \(S=\dfrac{a^3}{b}+\dfrac{b^3}{c}+\dfrac{c^3}{a}\ge2\left(ab+bc+ca\right)-ab+bc+ca=ab+bc+ca\)
suy ra BĐT ban đầu đúng
dấu = xảy ra khi và chỉ khi a=b=c.
P/s: cách khác :Áp dụng BĐT cauchy-schwarz:
\(\dfrac{a^3}{b}+\dfrac{b^3}{c}+\dfrac{c^3}{a}=\dfrac{a^4}{ab}+\dfrac{b^4}{bc}+\dfrac{c^4}{ca}\ge\dfrac{\left(a^2+b^2+c^2\right)^2}{ab+bc+ca}\)
\(S\ge\dfrac{\left(ab+bc+ca\right)^2}{ab+bc+ca}=ab+bc+ca\)
Câu hệ này =))
b, Từ hệ đã cho ta thấy x,y > 0
Trừ vế cho vế pt (1) và (2) của hệ ta được:
\(x^4-y^4=4y-4x\)
\(\Leftrightarrow\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)=4\left(y-x\right)\)
\(\Leftrightarrow\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)+4\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left[\left(x+y\right)\left(x^2+y^2\right)+4\right]=0\)
\(\Leftrightarrow x-y=0\) ( Vì \(\left(x+y\right)\left(x^2+y^2\right)+4>0\) với x,y > 0)
\(\Leftrightarrow x=y\)
Với x = y thay vào pt đầu của hệ ta được:
\(x^4-4x+3=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^3+x^2+x-3\right)=0\)
\(\Leftrightarrow\left(x-1\right)^2\left(x^2+2x+3\right)=0\)
\(\Leftrightarrow x-1=0\) ( Vì \(x^2+2x+3>0\) )
\(\Leftrightarrow x=1\)
Với x=1 suy ra y=1
Vậy hệ đã cho có nghiệm duy nhất (x;y) = (1;1)
Bài này mình làm lâu rồi á bann sửa dấu `2a+3b<=4` thành `2a+3b=4` nhé!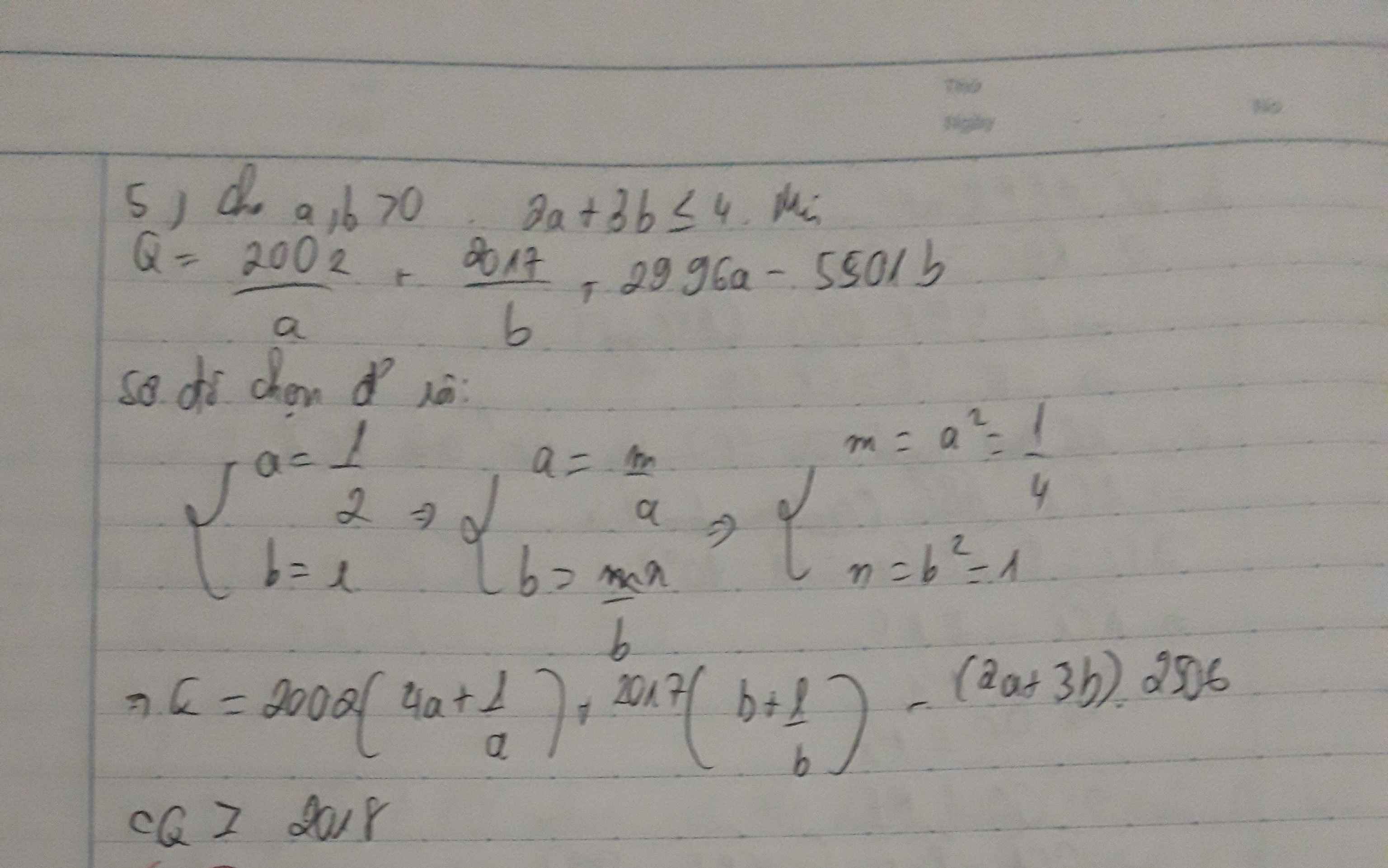
Bài này mình làm lâu rồi á bann sửa dấu 2a+3b≤42a+3b≤4 thành 2a+3b=42a+3b=4 nhé!
Là 2a+3b≤42a+3b≤4 ⇒ 2a+3b=42a+3b=4
hay 2a+3b=42a+3b=4 ⇒ 2a+3b≤42a+3b≤4