Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét (O) có
\(\widehat{BCD}\) là góc nội tiếp chắn \(\stackrel\frown{BD}\)
\(\widehat{ACD}\) là góc nội tiếp chắn \(\stackrel\frown{AD}\)
\(\stackrel\frown{BD}=\stackrel\frown{AD}\)(D là điểm nằm chính giữa của cung AB)
Do đó: \(\widehat{BCD}=\widehat{ACD}\)(Hệ quả góc nội tiếp)
mà tia CD nằm giữa hai tia CA và CB
nên CD là tia phân giác của \(\widehat{BCA}\)(đpcm)

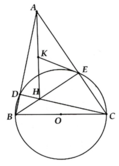
a, HS tự chứng minh
b, HS tự chứng minh
c, DAEH vuông nên ta có: KE = KA = 1 2 AH
=> DAKE cân tại K
=> K A E ^ = K E A ^
DEOC cân ở O => O C E ^ = O E C ^
H là trực tâm => AH ^ BC
Có A E K ^ + O E C ^ = H A C ^ + A C O ^ = 90 0
(K tâm ngoại tiếp) => OE ^ KE
d, HS tự làm
Bài 2:
Kẻ OH⊥AB tại H và OK⊥CD tại K
Ta có: OH⊥AB(gt)
AB//CD(gt)
Do đó: OH⊥CD(Định lí 2 từ vuông góc tới song song)
mà OK⊥CD(gt)
và OH và OK có điểm chung là O
nên O,H,K thẳng hàng
Xét ΔOAB có OA=OB(=R)
nên ΔOAB cân tại O(Định nghĩa tam giác cân)
Ta có: ΔOAB cân tại O(cmt)
mà OH là đường cao ứng với cạnh đáy AB(gt)
nên OH là đường phân giác ứng với cạnh AB(Định lí tam giác cân)
Suy ra: \(\widehat{AOH}=\widehat{BOH}\)
hay \(\widehat{AOK}=\widehat{BOK}\)
Xét ΔOCD có OC=OD(=R)
nên ΔOCD cân tại O(Định nghĩa tam giác cân)
Ta có: ΔOCD cân tại O(cmt)
mà OK là đường cao ứng với cạnh đáy CD(Gt)
nên OK là đường phân giác ứng với cạnh CD(Định lí tam giác cân)
hay \(\widehat{COK}=\widehat{DOK}\)
Ta có: \(\widehat{AOK}=\widehat{BOK}\)(cmt)
\(\widehat{COK}=\widehat{DOK}\)(cmt)
Do đó: \(\widehat{AOK}-\widehat{COK}=\widehat{BOK}-\widehat{DOK}\)
\(\Leftrightarrow\widehat{AOC}=\widehat{BOD}\)
\(\Leftrightarrow sđ\stackrel\frown{AC}=sđ\stackrel\frown{BD}\)
hay \(\stackrel\frown{AC}=\stackrel\frown{BD}\)(đpcm)