

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


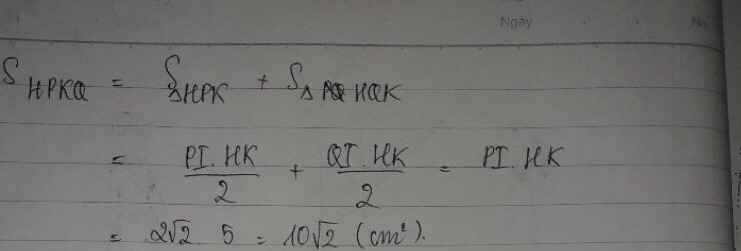

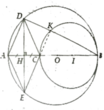
a, (O) và (I) tiếp xúc trong với nhau
b, Tứ giác ADCE là hình thoi
c, Có CK ⊥ AB, AD ⊥ DB
=> CK//AD mà CE//AD
=> B,K,D thẳng hàng
d, H K D ^ = H D K ^ ; I K B ^ = I B K ^
=> H K D ^ + I K B ^ = I B K ^ + H D K ^ = 90 0
=> I K H ^ = 90 0

a) Ta thấy ngay do BD, CE là đường cao nên \(\widehat{BEC}=\widehat{BDC}=90^o\)
Xét tứ giác AEDC có \(\widehat{BEC}=\widehat{BDC}=90^o\) nên AEDC là tứ giác nội tiếp hay A, E, D, C cùng thuộc một đường tròn.
Đường tròn cần tìm là đường tròn đường kính BC, tức là tâm đường tròn là trung điểm J của BC, bán kính là JB.
b) Xét tam giác BEC và tam giác BHM có :
\(\widehat{BEC}=\widehat{BHM}=90^o\)
Góc B chung
\(\Rightarrow\Delta BEC\sim\Delta BHM\left(g-g\right)\)
\(\Rightarrow\frac{BE}{BH}=\frac{BC}{BM}\Rightarrow BC.BH=BE.BM\)
Ta có \(BK^2=BD^2=BH.BC=BE.EM\) mà \(KE\perp BM\Rightarrow\widehat{BKM}=90^o\)
Vậy MK là tiếp tuyến của đường tròn tâm B.
c)
Gọi F là giao điểm của CE với đường tròn tâm B.
Do \(BE\perp KF\)nên MB là trung trực của FK.
\(\Rightarrow\widehat{MFB}=\widehat{MKB}=90^o\Rightarrow\)tứ giác MFBH nội tiếp.
\(\Rightarrow\widehat{MHF}=\widehat{MBF}\) (Hai góc nội tiếp cùng chắn cung MF)
Ta cũng có MKHB nội tiếp nên \(\widehat{MHK}=\widehat{MBK}\)
Mà \(\widehat{MBF}=\widehat{MBK}\) nên HI là phân giác góc KHF.
Áp dụng tính chất tia phân giác ta có : \(\frac{IK}{IF}=\frac{HK}{HF}\)
Ta có \(HC\perp HI\) nên HC là tia phân giác ngoài của góc KHF.
\(\Rightarrow\frac{CK}{CF}=\frac{HK}{HF}\)
Vậy nên \(\frac{CK}{CF}=\frac{IK}{IF}\)
\(\Rightarrow\frac{CK}{CF+KF}=\frac{IK}{IF+IK}\Rightarrow\frac{CK}{\left(CE+EF\right)+\left(CE-KE\right)}=\frac{IK}{FK}\)
\(\Rightarrow\frac{CK}{2CE}=\frac{IK}{2EK}\Rightarrow CK.EK=CE.IK\)

a) Ta có : OB - O'B = OO'
=> đường tròn (O) và (O'O tiếp xúc trong
b) Ta có : \(OA\perp DE\left(gt\right)\)
=> HD = HE hay H là trung điểm của DE
Theo (gt) : HA = HC
T/g ADCE có 2 đường chéo vuông góc với nhau tại trung điểm mỗi đường
=> T/g ADCE là hình thoi
c) Xét tam giác KBC có :
O'K = O'B = O'C (=bk)
\(\Rightarrow O'K=\frac{1}{2}BC\)
=> Tam giác KBC vuông tại K => \(CK\perp DB\left(1\right)\)
Xét tam giác ADB có :
OD = OA = OB ( =bk )
\(\Rightarrow OD=\frac{1}{2}AB\)
=> Tam giác ADB vuông tại D \(\Rightarrow AD\perp DB\left(2\right)\)
Từ (1) và (2) => CK // AD (*)
Theo ( c/m câu a ) : Tứ giác ADCE là hình thoi
=> CE // AD ( ** )
Từ (*) và (**) => CE và CK là 2 đường thẳng trùng nhau
Vậy : 3 điểm E , C , K thẳng hàng ( đpcm )
a. hai đường tròn tiếp xúc trong
b.ADCE là tứ giác thoi do có hai đường chéo vuông góc vcowis nhau tại trung điểm của mỗi đường
c. ta dễ thấy AD//CẺ mà AE vuông gó c với BD nên CE vuông BD
mà CK cũng vuông góc với BD nến C,K,E thẳng hàng
d. ta có do tam giác EKD vuông nên \(HK^2=HD^2=HA.HB=HC.HB\)
do \(HK^2=HC.HB\) nên HK là tiếp tuyến của O'