
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
Gọi R và h lần lượt là bán kính và chiều cao của 1 thùng sơn
Suy ra dung tích 1 thùng sơn: V = πR 2 h = 0 , 005 m 3
Gọi n là số thùng sơn tối đa sản xuất được
Tổng chi phí đó bỏ ra là: T = n × 100 . 000 × S x q + 120 . 000 × S d
= n × 100 . 000 × 2 πRh + 120 . 000 × 2 πR 2 ≤ 10 9 ⇔ n ≤ 5 × 10 4 π 10 × Rh + 12 × R 2
Mà 10 R h + 12 R 2 = 5 R h + 5 R h + 12 R 2 ≥ 3 300 R 4 h 2 3 = 3 300 V 2 π 2 3
⇒ n ≤ 5 × 10 4 π 10 × Rh + 12 × R 2 ≤ 5 × 10 4 π 3 × 300 V 2 π 2 3 ≈ 58135 , 9 ⇒ n = 58135 .

Đáp án C
Ta có: x 2 − x + 1 20 có số hạng tổng quát là C 20 k x 2 − x k
Mặt khác x 2 − x k có số hạng tổng quát là C k i x 2 i . − x k − i = C k i x k + i . − 1 k − i
Do đó số hạng tổng quát của khai triển là C 20 k . C k i . x k + i − 1 k − i (với k ; i ∈ ℕ ; i ≤ k ≤ 20 )
Với k + i = 3 ⇒ i = 0 ; k = 3 i = 1 ; k = 2
Hệ số bằng C 20 3 . C 3 0 . − 1 3 + C 20 2 . C 2 1 . − 1 1 = − 1520

a: =>1+2+...+x=120
=>x(x+1)/2=120
=>x(x+1)=240
=>\(x^2+x-240=0\)
\(\Delta=1^2-4\cdot1\cdot\left(-240\right)=961>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-1-31}{2}=\dfrac{-32}{2}=-16\left(loại\right)\\x_2=\dfrac{-1+31}{2}=15\left(nhận\right)\end{matrix}\right.\)


Đáp án B
Ta có: 2 x - 1 20 = ∑ k = 0 20 C 20 k - 2 x k - 1 20 - k = ∑ k = 0 20 C 20 k - 1 20 - k 2 k x k ⇒ a 3 = C 20 3 - 1 20 - 3 . 2 3 = - 9120 .

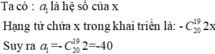
120 x 100 + 120 x 100 - 120 x 100
= (120 x 100) + (120 x 100) - (120 x 100)
= 12000 + 12000 - 12000
= 24000 - 12000
= 12000
12000