Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(M_Y=18.2=36\left(g/mol\right)\)
Đặt \(n_X=1\left(mol\right)\)
PTHH: \(X\xrightarrow[]{crackinh}ankan+anken\)
1---------->1---------->1
\(\Rightarrow m_X=m_Y=2.36=72\left(g\right)\\ \Rightarrow M_X=\dfrac{72}{1}=72\left(g/mol\right)\)
Đặt CTPT của X là CnH2n+2 (n ∈ N*)
`=> 14n + 2 = 72 => n = 5 (t//m)`
Vậy X là C5H12

X > Y + Z
a__a___a
Ya + Za / 2a = 36
>>1/2Y + 1/Z = 72
>>X=72 >>C5H12

Đặt \(m_{ankan}=100g\)
\(M_Y=2.14,5=29\)
\(\rightarrow n_Y=\frac{100}{29}mol\)
\(Ankan\rightarrow Ankan'+Anken\)
\(Ankan\rightarrow Anken+H_2\)
\(\rightarrow\text{Σ}n_{SP}=2n_{thamgia}\)
\(\rightarrow n_{crakingthamgia}=\frac{100}{29}mol\)
\(\rightarrow n_{ankanthamgia}=\frac{50}{29}mol\)
\(\rightarrow M_{ankan}=\frac{100}{\frac{50}{29}}=58g/mol\)
Vậy Ankan là \(C_4H_{10}\)

Đáp án : A
Gọi công thức phân tử của ankan X là CnH2n+2
Trong cùng điều kiện về nhiệt độ và áp suất thì tỉ lệ về thể tích cũng chính là tỉ lệ về số mol

=> mY = 24.nY = 24.3 = 72
Áp dụng định luật bảo toàn khối lượng ta có: mX = mY = 72
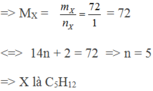

Ta có: \(\dfrac{n_t}{n_s}=\dfrac{M_s}{M_t}\Rightarrow\dfrac{1}{3}=\dfrac{12.2}{M_t}\Rightarrow M_t=72\)
Do đó X là $C_5H_{12}$
Khi mono clo hóa thu được $C_5H_{11}Cl$
$\Rightarrow \%m_{Cl}=33,3\%$
Khi monoclo hoá thu đc C5H11cl là sao vậy ạ ? E chưa rõ lắm đoạn này lắm:((

\(n_{Ankan}=\dfrac{11,2}{22,4}=0,5\left(mol\right)\)
\(M_{hhB}=1.29=29,n_B=\dfrac{22,4}{22,4}=1\left(mol\right)\)
=> \(m_{hhB}=1.29=29\left(g\right)\)
Bảo toàn khối lượng => \(m_{Akan}=m_{hhB}=29\left(g\right)\)
=> \(M_{Ankan}=\dfrac{29}{0,5}=58\)
Vậy Ankan cần tìm là C4H10
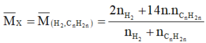
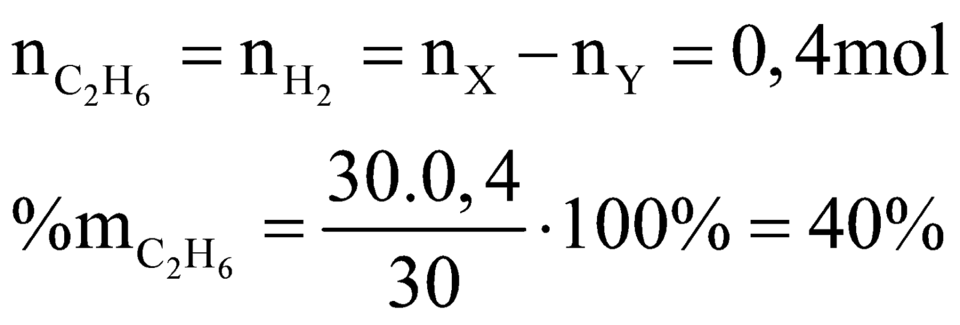
Ta có: \(\dfrac{n_t}{n_s}=\dfrac{M_s}{M_t}\Rightarrow\dfrac{1}{2}=\dfrac{18.2}{M_t}\Rightarrow M_t=72\) (Do cracking hoàn toàn)
Do đó X là $C_5H_{12}$. Không phân nhánh vậy X là pentan
\(CT:C_nH_{2n+2}\left(1mol\right)\)
\(C_nH_{2n+2}\underrightarrow{t^0,xt}C_aH_{2a+2}+C_bH_{2b}\left(n=a+b\right)\)
\(1...........................1.............1\)
\(m_Y=2\cdot2\cdot18=72\left(g\right)\)
\(BTKL:\)
\(m_X=m_Y=72\left(g\right)\)
\(\Rightarrow M_X=14n+2=72\left(\dfrac{g}{mol}\right)\)
\(\Rightarrow n=5\)
\(heptan\)