Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: (d)//(d1)
=>(d): y=-2x+b
Thay x=2 và y=-3 vào (d), ta được:
b-4=-3
=>b=1
b: Vì (d) vuông góc (d2)
nên (d): y=x+b
Thay x=-1 và y=-2 vào (d), ta được:
b-1=-2
=>b=-1

\(A\left(\sqrt{3}-\sqrt{2};1-\sqrt{6}\right)\in\left(d\right)\\ \Leftrightarrow\left(\sqrt{3}-\sqrt{2}\right)a+b=1-\sqrt{6}\left(1\right)B\left(\sqrt{2};2\right)\in\left(d\right)\\ \Leftrightarrow a\sqrt{2}+b=2\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}a\sqrt{3}-a\sqrt{2}+b=1-\sqrt{6}\\a\sqrt{2}+b=2\end{matrix}\right.\)
Lấy 2 PT trừ nhau
\(\Leftrightarrow a\left(2\sqrt{2}-\sqrt{3}\right)=1+\sqrt{6}\\ \Leftrightarrow a=\dfrac{\sqrt{6}+1}{2\sqrt{2}-\sqrt{3}}=\dfrac{\left(\sqrt{6}+1\right)\left(2\sqrt{2}+\sqrt{3}\right)}{8-3}\\ \Leftrightarrow a=\dfrac{11\sqrt{2}+\sqrt{3}}{5}\\ \Leftrightarrow b=2-a\sqrt{2}=\dfrac{10-\sqrt{2}\left(11\sqrt{2}+\sqrt{3}\right)}{5}\\ \Leftrightarrow b=\dfrac{-12-\sqrt{6}}{5}\)

a. Em tự giải
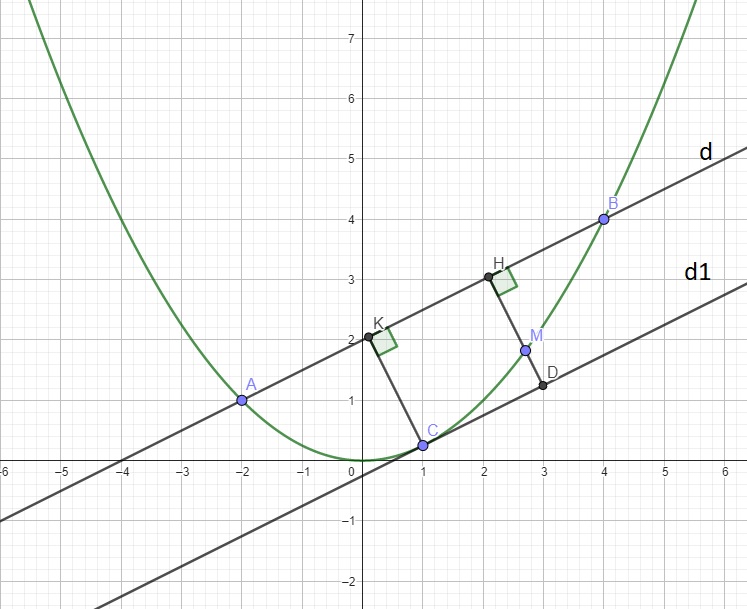
b. Từ giả thiết ta có \(A\left(-2;1\right)\) và \(B\left(4;4\right)\)
Gọi phương trình (d) có dạng \(y=ax+b\), do (d) qua A và B nên:
\(\left\{{}\begin{matrix}-2a+b=1\\4a+b=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=2\end{matrix}\right.\) \(\Rightarrow y=\dfrac{1}{2}x+2\)
c. Câu này có vài cách giải cho lớp 9, cách nhanh nhất là sử dụng tính chất tiếp tuyến.
Từ M kẻ \(MH\perp AB\Rightarrow S_{ABM}=\dfrac{1}{2}MH.AB\)
Do AB cố định \(\Rightarrow S_{max}\) khi \(MH_{max}\)
Gọi \(d_1\) là đường thẳng song song d và tiếp xúc (P), gọi C là tiếp điểm \(d_1\) và (P)
Do \(d_1\) song song (d) nên pt có dạng: \(y=\dfrac{1}{2}x+b\)
Phương trình hoành độ giao điểm \(d_1\) và (P):
\(\dfrac{1}{4}x^2=\dfrac{1}{2}x+b\Rightarrow x^2-2x-4b=0\) (1)
Do \(d_1\) tiếp xúc (P) \(\Rightarrow\left(1\right)\) có nghiệm kép
\(\Rightarrow\Delta'=1+4b=0\Rightarrow b=-\dfrac{1}{4}\)
Thế vào (1) \(\Rightarrow x_C^2-2x_C+1=0\Rightarrow x_C=1\Rightarrow y_C=\dfrac{1}{4}\) \(\Rightarrow C\left(1;\dfrac{1}{4}\right)\)
Từ C kẻ \(CK\perp d\)
Giả sử HM kéo dài cắt \(d_1\) tại D \(\Rightarrow\) tứ giác CKHD là hình chữ nhật (2 cặp cạnh đối song song và 1 góc vuông)
\(\Rightarrow CK=DH\)
Mà \(DH=MH+MD\ge MH\Rightarrow CK\ge MH\)
\(\Rightarrow MH_{max}=CK\) khi M trùng C
Hay \(M\left(1;\dfrac{1}{4}\right)\)

Bài 2 :
\(\hept{\begin{cases}3x+2y=11\left(1\right)\\x+2y=5\left(2\right)\end{cases}}\)
Lấy phương trình (1) - phương trình (2) ta được :
\(2x=6\Leftrightarrow x=3\)
Thay x = 3 vào phương trình (2) ta được :
\(3+2y=5\Leftrightarrow2y=2\Leftrightarrow y=1\)
Vậy \(\left(x;y\right)=\left(3;1\right)\)

a, Cho pt đt (d) có dạng y = ax + b
(d) đi qua N(2;3) => 3 = 2a + b
(d) // y = 2x - 5 <=> \(\left\{{}\begin{matrix}a=2\\b\ne-5\end{matrix}\right.\)
Thay a = 2 ta được : 3 = 4 + b => b = -1 (tmđk )
Vậy ptđt (d) có dạng y = 2x - 1
b, Hoành độ giao điểm tm pt
\(x^2-2x-3=0\)ta có : a - b + c = 0
Vậy pt có 2 nghiệm \(x_1=-1;x_2=3\)
Với x = -1 => y = 1
Với x = 3 => y = 9
Vậy A(-1;1) ; B(3;9)
c, Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=-5\end{matrix}\right.\)
Ta có : \(A=\left(x_1+x_2\right)^2-3x_1x_2\)
Thay vào ta được :
\(A=4-3\left(-5\right)=19\)

xin lỗi mình chưa đọc chỗ parabol ,sửa dòng 8 dưới lên nhé
\(x_1x_2\left(\frac{1}{2}x_1^2+\frac{1}{2}x_2^2\right)+48=0\)
\(\Leftrightarrow\frac{1}{2}x_1x_2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]+48=0\)
\(\Leftrightarrow\frac{1}{2}\left(2m-2\right)\left[16-2\left(2m-2\right)\right]+48=0\)
\(\Leftrightarrow\left(m-1\right)\left(20-4m\right)+48=0\Leftrightarrow-4m^2+20m-20+4m+48=0\)
\(\Leftrightarrow-4m^2+24m+28=0\Leftrightarrow m^2-6m-7=0\)
Ta có : a - b + c = 1 + 6 - 7 = 0
vậy pt có nghiệm x = -1 ; x = 7
a) vì A(-1; 3) thuộc (d) nên:
3 = 2.(-1) - a + 1
<=> 3 = -2 - a + 1
<=> a = 4
b) Lập phương trình hoành độ giao điểm:
\(2x-a+1=\frac{1}{2}x^2\)
\(\Leftrightarrow\frac{1}{2}x^2-2x+a-1=0\)
ta có: \(y_1=\frac{1}{2}x_1^2\)
\(y_2=\frac{1}{2}x_2^2\)
\(\Leftrightarrow x_1x_2\left(\frac{1}{2}x_1^2+\frac{1}{2}x_2^2\right)+48=0\)
\(\Leftrightarrow x_1x_2\left[\frac{1}{2}\left(x_1^2+x_2^2\right)\right]+48=0\)
\(\Leftrightarrow x_1x_2\left[\frac{1}{2}\left(x_1+x_2\right)^2-2x_1x_2\right]+48=0\)
Theo định lý viet, ta có: \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=4\\x_1x_2=\frac{c}{a}=\frac{a-1}{2}\end{cases}}\)
\(\Leftrightarrow\left(\frac{a-1}{2}\right)\left[\frac{1}{2}\cdot4^2-2\left(\frac{a-1}{2}\right)\right]+48=0\)
\(\Leftrightarrow10a-a^2+87=0\)
\(\Leftrightarrow\orbr{\begin{cases}x_1=5-4\sqrt{7}\\x_2=5+4\sqrt{7}\end{cases}}\)



a: (d): y=ax+b
Theo đề, ta có hệ:
a+b=3 và 2a+b=4
=>a=1 và b=2
b: Theo đề, ta có hệ:
-3a+b=2 và 2a+b=3
=>a=1/5 và b=13/5