Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

7,2km/h = 2 m/s
72km/h = 20 m/s
Chọn chiều dương là chiều lên dốc, gốc tọa độ tại chân dốc, ta có :
Phương trình tọa độ của xe ô tô là:
x = 20.t + 0,4.t²/2 = 20t + 0,2t² (1)
Phương trình tọa độ của xe đạp là:
x' = 570 - 2.t - 0,2.t²/2 = 570 - 2t - 0,1t² (2) ( lấy v < 0 và a < 0 do nó có hướng ngược chiều dương )
Hai xe gặp nhau khi x = x'
=> 20t + 0,2t² = 570 - 2t - 0,1t²
<=> 0,3t² + 22t - 570 = 0
∆' = 11² - 0,3.(- 570) = 292
=> t = 20,3 (s)
=> x = 20.20,3 + 0,2.(20,3)² = 488,4 (m)
Vậy hai xe gặp nhau lúc t = 20,3 (s) và cách chân dốc x = 488,4 (m)
b)
Quãng đường ô tô đi được khi gặp nhau là:
s2 = x = 488,4 (m)
Vận tốc ô tô lúc đó là:
v2 = vo2 + at = 20 + 0,4.20,3 = 28,12 (m/s)
Quãng đường xe đạp đi được khi gặp nhau là:
s1 = 570 - 488,4 = 81,6 (m)
Vận tốc xe đạp lúc đó là:
v1 = vo1 + at = 2 + 0,2.20,3 = 6,06 (m/s)

- Chọn gốc tọa độ và gốc thời gian lần lượt là nơi và lúc người đi xe đạp bắt đầu xuống dốc. Chiều dương trùng với chiều của người đi xe đạp.
- Đổi 7,2km/h =2m/s
- Phương trình chuyển động của xe đạp: xA = 2t + 0,1t2
Phương trình chuyển động của ô tô: xB = 570 - 20t - 0,2t2
- 2 xe gặp nhau \(\Leftrightarrow\) xA = xB
\(\Leftrightarrow\) 2t + 0.1t2 = 570 - 20t - 0,2t2
\(\Leftrightarrow\) t \(\simeq\) 20,3 s
\(\Rightarrow\)xA = xB = 81,809 (m) = sA
2 xe cách nhau 170m \(\Rightarrow\left|x_A-x_B\right|=170\)
Giải ra thôi!!
À nhầm chút.....![]() xB=570-20t+0.2t2 nhé..... ko đọc kỹ đề bài =))
xB=570-20t+0.2t2 nhé..... ko đọc kỹ đề bài =))

Chọn A.
Chọn chiều dương là chiều từ đỉnh đến chân dốc, gốc toạ độ tại đỉnh A, gốc thời gian là lúc xe A xuống dốc.
Đối với xe A:
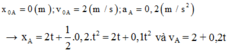
Đối với xe B:
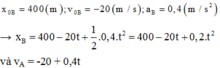
Để hai xe cách nhau 40m thì
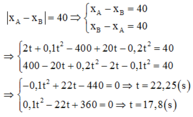

Giải:
Chọn chiều dương là chiều từ đỉnh đến chân dốc, gốc toạ độ tại đỉnh A, gốc thời gian là lúc xe A xuống dốc.
Đối với xe A:
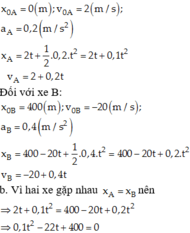

Thay thời gian loại nghiệm ta có hai thời điểm vật cách nhau 40m là

Đáp án:
Giải thích các bước giải:
a) Phương trình chuyển động của mỗi xe:
Chọn trục toạ độ trùng với dốc, gốc toạ độ tại chân dốc, chiều dương là chiều chuyển động của ô tô, gốc thời gian là lúc ô tô bắt đầu lên dốc.
+ Đối với xe đạp ta có:
Phương trình chuyển động của xe đạp là:
+ Đối với ô tô ta có:
Phương trình chuyển động của ô tô là:
b) Quãng đường đi được của ô tô được xác định bởi công thức:

Câu này mk đã vt pt chuyển động r, vậy để 2 xe cách nhau 170m
\(\Leftrightarrow\left|x_A-x_B\right|=170\)
\(\Leftrightarrow\left[{}\begin{matrix}2t+0,1t^2-570+20t-0,2t^2=170\\2t+0,1t^2-570+20t-0,2t^2=-170\end{matrix}\right.\)
Giải ra sẽ ra t, thay vào 1 trong 2 pt chuyển động của xe đạp hoặc xe ô tô sẽ ra vị trí

Chọn vị trí xe đạp bắt xuống dốc là gốc toạ độ, chiều từ đỉnh dốc đến chân dốc
Xét xe A: \(\left\{{}\begin{matrix}v_{0A}=7,2\left(km/h\right)=2m/s\\a=0,2m/s^2\\x_{0A}=0\end{matrix}\right.\)
PT chuyển động xe đạp: \(x_A=x_{0A}+v_{0A}.\left(t-t_{0A}\right)+\frac{1}{2}a\left(t-t_{0A}\right)^2\)
\(\Leftrightarrow x_A=2t+\frac{1}{2}.0,2.t^2=2t+0,1.t^2\)
Xét xe ô tô: \(\left\{{}\begin{matrix}v_{0B}=72\left(km/h\right)=20\left(m/s\right)\\a=0,4\left(m/s\right)\\x_{0B}=570\left(m\right)\end{matrix}\right.\)
\(\Rightarrow x_B=x_{0B}+v_{0B}\left(t-t_{0B}\right)+\frac{1}{2}a\left(t-t_{0B}\right)^2\)
\(\Leftrightarrow x_B=570+20t+\frac{1}{2}.0,4.t^2=570-20t+0,2.t^2\)
Để 2 xe gặp nhau: xA=xB
\(\Leftrightarrow2t+0,1.t^2=570-20t+0,2.t^2\)
\(\Leftrightarrow0,1.t^2-22t+570=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=190\left(s\right)\\t=30\left(s\right)\end{matrix}\right.\)
Vs t= 190(s)=> quãng đg xe đạp đi là: ...
Vs t= 30s=> quãng đg...
b/ PT vận tốc của xe đạp: \(v_A=v_{0A}+a\left(t-t_{0A}\right)=2+0,2t\)
\(v_B=v_{0B}+a\left(t-t_{0B}\right)=-20+0,4t\)
2 xe có tốc độ = nhau: \(v_A=v_B\Leftrightarrow2+0,2t=0,4t-20\)
\(\Leftrightarrow t=110\left(s\right)\)
câu c đb ko rõ ràng là cách nhau bn