Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(VT=\frac{2\left(\sqrt{2}-\sqrt{1}\right)}{3.\left(2-1\right)}+\frac{2\left(\sqrt{3}-\sqrt{2}\right)}{5\left(3-2\right)}+...+\frac{2\left(\sqrt{2006}-\sqrt{2005}\right)}{4011\left(2006-2005\right)}\)
\(VT=\frac{2\left(\sqrt{2}-\sqrt{1}\right)}{3}+\frac{2\left(\sqrt{3}-\sqrt{2}\right)}{5}+...+\frac{2\left(\sqrt{2006}-\sqrt{2005}\right)}{4011}\)
Nhận xét: (a-b)2 \(\ge\) 0 => a2 + b2 \(\ge\) 2ab
Áp dụng ta có: \(3=\left(\sqrt{2}\right)^2+\left(\sqrt{1}\right)^2\ge2.\sqrt{2}.\sqrt{1}\)
\(5=\left(\sqrt{3}\right)^2+\left(\sqrt{2}\right)^2\ge2.\sqrt{3}.\sqrt{2}\)
...
\(4011=\left(\sqrt{2006}\right)^2+\left(\sqrt{2005}\right)^2\ge2.\sqrt{2006}.\sqrt{2005}\)
=> \(VT

Hai bài này áp dụng hằng đẳng thức \(a^2-b^2=\left(a-b\right)\left(a+b\right)\) bạn nhé
a)
\(\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)\)
\(=2^2-\sqrt{3}^2\)
\(=4-3\)
\(=1\)
b)
Hai số nghịch đảo nhau là 2 số có tích của chúng bằng 1
Ví dụ
\(\frac{a}{b}\) và \(\frac{b}{a}\) ( hai số nghịch đảo )
\(\frac{a}{b}.\frac{b}{a}=1\)
Ta có
\(\left(\sqrt{2006}-\sqrt{2005}\right)\left(\sqrt{2006}+\sqrt{2005}\right)\)
\(=\sqrt{2006}^2-\sqrt{2005}^2\)
\(=2006-2005\)
\(=1\)
=> Đpcm

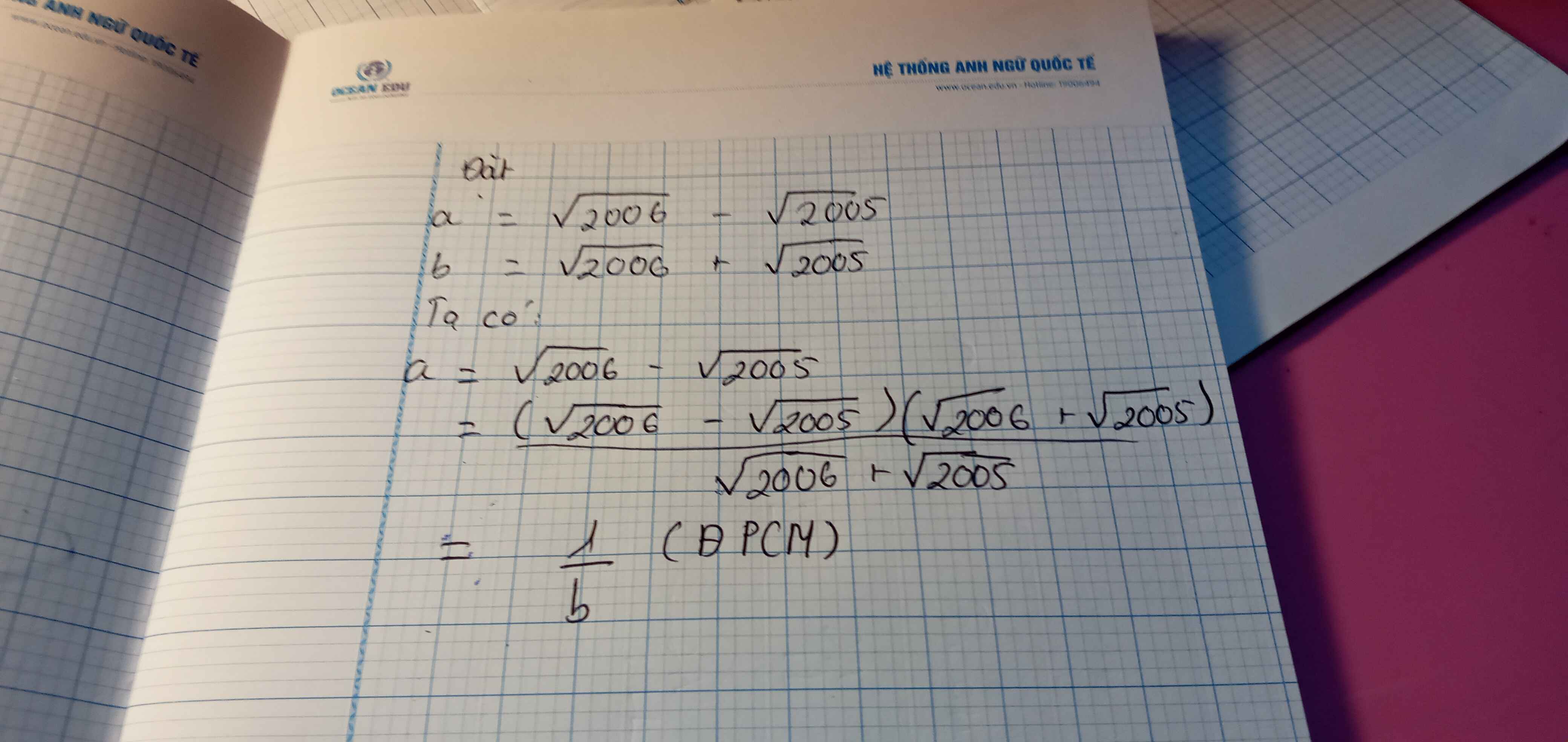
Đặt \(a=\sqrt{2006}-\sqrt{2005};b=\sqrt{2006}+\sqrt{2005}\)
Ta có
\(a=\sqrt{2006}-\sqrt{2005}=\dfrac{\left(\sqrt{2006}-\sqrt{2005}\right)\left(\sqrt{2006}+\sqrt{2005}\right)}{\sqrt{2006}+\sqrt{2005}}=\dfrac{1}{b}\)
\(\RightarrowĐfcm\)

Câu 4: a) ĐK: \(x^2\ge9\Leftrightarrow\left[{}\begin{matrix}x\ge3\\x\le-3\end{matrix}\right.\)
b) ĐK: \(x^2-3x+2\ge0\Leftrightarrow\left[{}\begin{matrix}x\le1\\x\ge2\end{matrix}\right.\)
c) Đk: \(-3\le x< 5\)
d) x + 3 và 5 - x đồng dấu. Xét hai trường hợp:
\(\left\{{}\begin{matrix}x+3\ge0\\5-x>0\left(\text{do mẫu phải khác 0}\right)\end{matrix}\right.\Leftrightarrow-3\le x< 5\)
\(\left\{{}\begin{matrix}x+3< 0\\5-x< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< -3\\x>5\end{matrix}\right.\) do x ko thể đồng thời thỏa mãn cả hai nên loại.
Câu 1:
a) Đặt \(A=x+\sqrt{\left(x+2\right)^2}\cdot\left(x-2\right)\)
\(A=x+\left|x+2\right|\cdot\left(x-2\right)\)
+) Với \(x\ge-2\):
\(A=x+\left(x+2\right)\left(x-2\right)=x+x^2-4\)
+) Với \(x< -2\):
\(A=x-\left(x+2\right)\left(x-2\right)=x-x^2+4\)
b) \(B=\sqrt{m^2-6m+9-2m}\)
\(B=\sqrt{m^2-8m+9}\)
Bạn xem lại đề nhé :)
c) \(C=1+\sqrt{\frac{\left(x-1\right)^2}{x-1}}\)
\(C=1+\sqrt{x-1}\)
d) \(D=\sqrt{x+4\sqrt{x-4}}+\sqrt{x-4\sqrt{x-4}}\)
\(D=\sqrt{x-4+4\sqrt{x-4}+4}+\sqrt{x-4-4\sqrt{x-4}+4}\)
\(D=\sqrt{\left(\sqrt{x-4}+2\right)^2}+\sqrt{\left(\sqrt{x-4}-2\right)^2}\)
\(D=\sqrt{x-4}+2+\left|\sqrt{x-4}-2\right|\)
+) Xét \(x\ge8\):
\(D=\sqrt{x-4}+2+\sqrt{x-4}-2=2\sqrt{x-4}\)
+) Xét \(4< x< 8\):
\(D=\sqrt{x-4}+2+2-\sqrt{x-4}=4\)
Vậy....

a: Ta có: \(\sqrt{\left(5-\sqrt{19}\right)^2}-\sqrt{\left(4-\sqrt{19}\right)^2}\)
\(=5-\sqrt{19}-\sqrt{19}+4\)
\(=9-2\sqrt{19}\)
b: Ta có: \(\sqrt{\left(3-2\sqrt{2}\right)^2}-\sqrt{\left(2\sqrt{2}-3\right)^2}\)
\(=3-2\sqrt{2}-3+2\sqrt{2}\)
=0
c.
Căn bậc 2 không xác định do $2-\sqrt{5}< 0$
d.
\(=\sqrt{(3+\sqrt{3})^2}(3+\sqrt{3})=|3+\sqrt{3}|(3+\sqrt{3})=(3+\sqrt{3})^2=12+6\sqrt{3}\)
e.
\(=(2-\sqrt{5})\sqrt{(2+\sqrt{5})^2}=(2-\sqrt{5})|2+\sqrt{5}|=(2-\sqrt{5})(2+\sqrt{5})=4-5=-1\)
a)\(\sqrt{\left(13+12\right)\left(13-12\right)}=\sqrt{25}+\sqrt{1}=5+1=6\)=6 ( hằng đẳng thức số 3) \(a^2-b^2=\left(a+b\right)\left(a-b\right)\)
b) tương tự
a) \(\sqrt{13^2-12^2}=\sqrt{\left(13-12\right)\left(13+12\right)}=\sqrt{25}=5\)
b) \(\sqrt{17^2-8^2}=\sqrt{\left(17-8\right)\left(17+8\right)}=\sqrt{25.9}=\sqrt{225}=15\)
c) \(\sqrt{117^2-108^2}=\sqrt{\left(117-108\right)\left(117+108\right)}=\sqrt{225.9}=\sqrt{2025}=45\)
d) \(\sqrt{313^2-312^2}=\sqrt{\left(313-312\right)\left(313+312\right)}=\sqrt{625}=25\)
mk nghi nhu vay ko biet co dung ko
dung thi bao mk nha