Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath

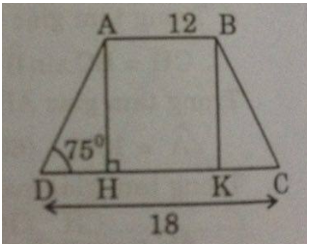
Giả sử hình thang cân ABCD có AB = 12cm, CD = 18cm,
Kẻ
Vì tứ giác ABKH là hình chữ nhật nên: AB = HK = 12 (cm)
Chúc bạn học tốt , bạn nhớ cho mình 1 like nhé !
Ta có: tam giác ADH = tam giác BCK (cạnh huyền, góc nhọn)
Suy ra: DH = CK
Suy ra:
Trong tam giác vuông ADH, ta có:
Vậy:
(cm2).
Tham khảo:

Giả sử hình thang cân ABCD có AB = 12cm, CD = 18cm,\(\widehat{D}\)\(=75^0\)
Kẻ AH ⊥ CD, BK ⊥ CD
Vì tứ giác ABKH là hình chữ nhật nên: AB = HK = 12 (cm)
Ta có: tam giác ADH = tam giác BCK (cạnh huyền, góc nhọn)
Suy ra: DH = CK
Suy ra: \(DH=\dfrac{CD-HK}{2}=\dfrac{18-12}{2}=3\) ( cm )
Trong tam giác vuông ADH, ta có:
\(AH=DH.tgD=3.tg75^0\approx11,196\) ( cm )
Vậy: \(S_{ABCD}=\dfrac{AB+CD}{2}.AH=\dfrac{12+18}{2}.11,196=167,94\) ( cm\(^2\) )


Giả sử hình thang cân ABCD có AB = 12cm, CD = 18cm, D^=75∘
Kẻ AH⊥CD,BK⊥CD
Vì tứ giác ABKH là hình chữ nhật nên: AB = HK = 12 (cm)
Ta có: tam giác ADH = tam giác BCK (cạnh huyền, góc nhọn)
Suy ra: DH = CK
Suy ra:
DH=CD–HK2=18–122=3(cm)
Trong tam giác vuông ADH, ta có:
AH=DH.tgD=3.tg75∘≈11,196(cm)
Vậy:
SABCD=AB+CD2.AH≈12+182.11,196=167,94 (cm2).

Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=5^2+12^2=169\)
hay BC=13cm
Ta có: ΔABC vuông tại A
nên bán kính đường tròn ngoại tiếp ΔABC là một nửa của cạnh huyền BC
hay \(R=\dfrac{BC}{2}=\dfrac{13}{2}=6.5\left(cm\right)\)
Bài 2:
Ta có: ABCD là hình thang cân
nên A,B,C,D cùng thuộc 1 đường tròn\(\left(đl\right)\)
hay bán kính đường tròn ngoại tiếp ΔABC cũng là bán kính đường tròn ngoại tiếp tứ giác ABCD
Xét ΔABC có
\(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Suy ra: Bán kính của đường tròn ngoại tiếp tứ giác ABCD là \(R=\dfrac{BC}{2}=10\left(cm\right)\)