Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

9187 -y : 409 = 892 - 102
<=> 9187 -y : 409 = 7819
<=> y : 409 = 9187 - 7819
<=> y : 409 = 1368
<=> y = 1368 . 409
<=> y = 559512
8.6+ 288: [x-3]2 = 50
48+288: [x-3]2 = 50
288: [x-3]2 = 50-48
288: [x-3]2 = 2
[x-3]2=144
x-3=12
x=15
633 .85 : x = 897
53805:x=897
x=17935/299

a) 60 - 3 ( x - 2 ) = 51
=> 3 (x - 2) = 60 - 51 = 9
=> x - 2 = 9 : 3 = 3
=> x = 3 = 2 = 5
b) 4x - 20 = 2^5 : 2^2
=> 4x - 20 = 8
=> 4x = 8 + 20 = 28
=> x = 28 : 4 = 7
c) 48751 - ( 10425 + x ) = 382^8 : 12
đề có sai ko ?
d) ( 2367 - x ) - ( 2^10 - 7 ) = 15^2 - 20
=> 2367 - x - 2^10 + 7 = 205
=> -x = 205 - 7 + 210 - 2367 = -1145
=> x = 1145
câu D của bạn trần như sai rồi phải là 1146 mới là đáp án đúng

a,(2x+1)(y-3)=12
⇒⇒2x+1 và y-3 ∈∈Ư(12)={±1;±2;±3;±4;±6;±12}{±1;±2;±3;±4;±6;±12}
| 2x+1 | 1 | -1 | 2 | -2 | 3 | -3 |
| y-3 | 12 | -12 | 6 | -6 | 4 | -4 |
| x | 0 | -1 | 1212 | −32−32 | 1 | -2 |
| y | 15 | -9 | 9 | 3 | 7 | -1 |
=>x=0,y=15
c) Ta có: \(36^{25}=\left(6^2\right)^{25}=6^{50}\)
\(25^{36}=\left(5^2\right)^{36}=5^{72}\)
Ta có: \(6^{50}=\left(6^5\right)^{10}=7776^{10}\)
mà \(5^{70}=\left(5^7\right)^{10}=78125^{10}\)
nên \(6^{50}< 5^{70}\)
mà \(5^{70}< 5^{72}\)
nên \(6^{50}< 5^{72}\)
hay \(36^{25}< 25^{36}\)

Tham khảo:
a)
( 2x + 1 ) . ( y - 3 ) = 12
Vì 2x +1 là số lẻ.
Do ( 2x + 1 ) . ( y - 3) = 12
=> 2x + 1 : y - 3 thuộc Ư ( 12) = { 1 ; 2 ; 3 ; 4 ; 6 ; 12 }
=> 2 x +1 = 1 => x= 0
hoặc y - 3 = 12 => y = 15
=> 2x + 1 = 3 => x = 2
hoặc y - 3 = 4 => y = 7
=> 2x + 1 = 2 ( L)
VẬY ( x ; y) = { ( 0 ; 15 ) ; ( 2 ; 7) }

a, Ta có: 42 = 2.3.7 = 1.42 = 2.21 = 3.14 = 6.7
Vì a < b nên ta tìm được các cặp số (a ;b) là (1;42), (2;21), (3;14), (6;7)
b, Ta có: 102 = 2.3.17 = 2.51 = 3.34 = 6.17
Vì x; y là số tự nhiên nên x + 5 ≥5 ; y + 2 ≥ 2. Khi đó (x+5)(y+2) = 51.2 = 34.3 = 6.17 = 17.6
Ta có bảng sau:
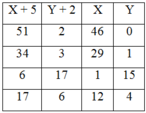
Vậy có các cặp nghiệm (x;y) thỏa mãn đề bài là: (46;0), (29;1), (1;15), (12;4)

các bạn nêu cách làm cụ thể giúp mình nha mình sẽ k cho
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

bài 3
( x + 5 ) . ( y + 2 ) = 102
ta có :\(y+2\inƯ\left(102\right)\)
mà \(y+2\ge2\)
nên \(y+2=2\)hoặc \(y+2=3\)
TH1 nếu \(y+2=2\)
=>\(y=1\)
Do \(y+2=2\)nên \(x+5=51\)
=>\(x=46\)
TH2 nếu \(y+2=3\)
=>\(y=1\)
Do \(y+2=3\)nên \(x+5=34\)
=>\(x=29\)
Vậy cặp số x;y lần lượt là :
nếu y=0 thì x=46
nếu y=1 thì x=29
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
Bài 1:
a: Ta có: \(48751-\left(10425+y\right)=3828:12\)
\(\Leftrightarrow y+10425=48751-319=48432\)
hay y=38007
b: Ta có: \(\left(2367-y\right)-\left(2^{10}-7\right)=15^2-20\)
\(\Leftrightarrow2367-y=1222\)
hay y=1145
Bài 2:
Ta có: \(8\cdot6+288:\left(x-3\right)^2=50\)
\(\Leftrightarrow288:\left(x-3\right)^2=2\)
\(\Leftrightarrow\left(x-3\right)^2=144\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=12\\x-3=-12\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=15\\x=-9\end{matrix}\right.\)