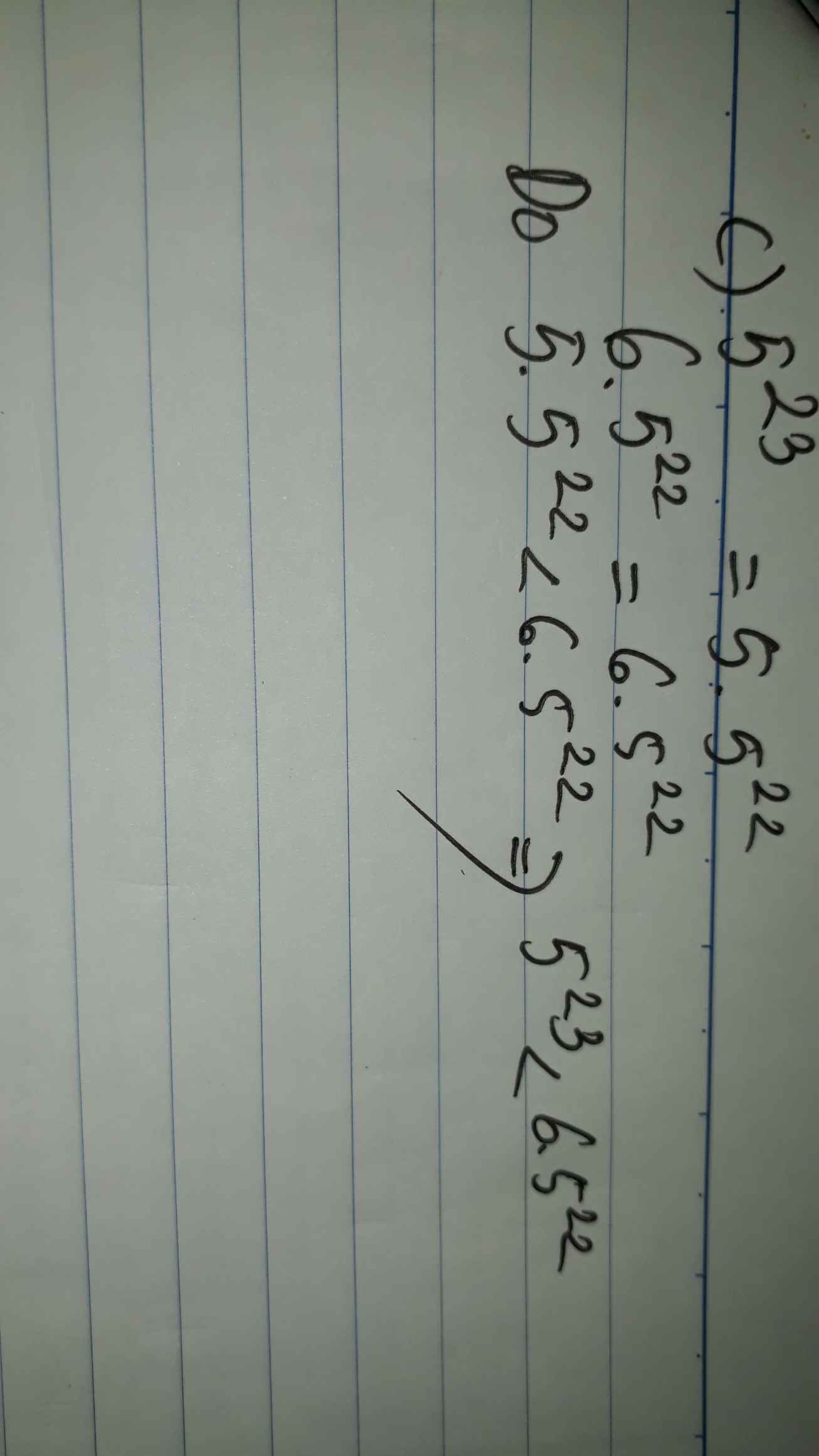Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,5mũ 36=(5mũ3)mũ12=125 mũ12
11^24=(11^2)12=121^12
vì 121<125 nên 5^36>11^24

Kiến thức: một số chính phương là một số chia hết cho 4 hoặc chia 4 dư 1
Bài giải
a) A = 3 + 32 + 33 + 34 +...+ 319 + 320
A = (3 + 32) + (33 + 34) +...+ (319 + 320)
A = (3.1 + 3.3) + (33.1 + 33.3) +...+ (319.1 + 319.3)
A = [3.(1 + 3)] + [33.(1 + 3)] +...+ [319.(1 + 3)]
A = 3.4 + 33.4 +...+ 319.4
A = (3 + 33 +...+ 319).4 chia hết cho 4
Vì A chia hết cho 4
Suy ra A là một số chính phương
b) B = 11 + 112 + 113
B = 11 + (112 + 113)
B = 11 + (112.1 + 112.11)
B = 11 + [112.(1 + 11)]
B = 11 + 112.12
Vì 112.12 chia hết cho 4
và 11 chia 4 dư 3
Nên B không phải là một số chính phương
Vậy B không phải là một số chính phương
a) A = 3 + 32 + 33 + ... + 320
Các lũy thừa của 3 từ 32 trở đi đều chia hết cho 9
=> 32; 33; ...; 320 chia hết cho 9
=> 32 + 33 + ... + 320 chia hết cho 9
Mà 3 chia hết cho 3 nhưng không chia hết cho 9
=> A chia hết cho 3 nhưng không chia hết cho 9, không là số chính phương
Câu b tương tự

Bài 1
a) \(x=x^5\)
\(x^5-x=0\)
\(x\left(x^4-1\right)=0\)
\(x=0\) hoặc \(x^4-1=0\)
* \(x^4-1=0\)
\(x^4=1\)
\(x=1\)
Vậy x = 0; x = 1
b) \(x^4=x^2\)
\(x^4-x^2=0\)
\(x^2\left(x^2-1\right)=0\)
\(x^2=0\) hoặc \(x^2-1=0\)
*) \(x^2=0\)
\(x=0\)
*) \(x^2-1=0\)
\(x^2=1\)
\(x=1\)
Vậy \(x=0\); \(x=1\)
c) \(\left(x-1\right)^3=x-1\)
\(\left(x-1\right)^3-\left(x-1\right)=0\)
\(\left(x-1\right)\left[\left(x-1\right)^2-1\right]=0\)
\(x-1=0\) hoặc \(\left(x-1\right)^2-1=0\)
*) \(x-1=0\)
\(x=1\)
*) \(\left(x-1\right)^2-1=0\)
\(\left(x-1\right)^2=1\)
\(x-1=1\) hoặc \(x-1=-1\)
**) \(x-1=1\)
\(x=2\)
**) \(x-1=-1\)
\(x=0\)
Vậy \(x=0\); \(x=1\); \(x=2\)

Ko ghi đề
\(2A=2+2^2+...+2^{101}\\ 2A-A=2^{101}-1\\ =>A=2^{101}-1\)
Mấy cái khác cg lm như v (b thì 3b)
Nhớ đúng mk nhá