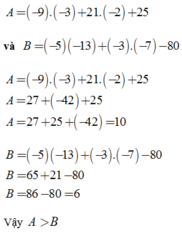K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
XO
6 tháng 8 2020
\(A=\left(\frac{1}{2^2}-1\right).\left(\frac{1}{3^2}-1\right)...\left(\frac{1}{100^2}-1\right)=\frac{-3}{2^2}.\frac{-8}{3^2}...\frac{-9999}{100^2}\)
\(=-\frac{3.8...9999}{2^2.3^2...100^2}=-\frac{1.3.2.4...99.101}{2.2.3.3...100.100}=-\frac{\left(1.2....99\right).\left(3.4...101\right)}{\left(2.3...100\right).\left(2.3...100\right)}=-\frac{1.101}{100.2}=-\frac{101}{200}\)
\(< -\frac{100}{200}=\frac{1}{2}=B\)
=> A < B
PT
1
CM
19 tháng 1 2019
A = − 9 . − 3 + 21. − 2 + 25 A = 27 + − 42 + 25 A = 27 + 25 + − 42 = 10 B = − 5 − 13 + − 3 . − 7 − 80 B = 65 + 21 − 80 B = 86 − 80 = 6
Vậy A > B
PT
1
PT
1
CM
9 tháng 6 2018
Thực hiện phép tính ta được A = l0 ; B = 6.
Từ đó suy ra A > B.
PT
1
PT
1
CM
27 tháng 9 2017
A = − 9 . − 3 + 21. − 2 + 25 A = 27 + − 42 + 25 A = 27 + 25 + − 42 = 10
B = − 5 − 13 + − 3 . − 7 − 80 B = 65 + 21 − 80 B = 86 − 80 = 6
Vậy A > B
PT
1
PT
1
CM
5 tháng 1 2020
Thực hiện phép tính ta được A = l0 ; B = 6.
Từ đó suy ra A > B.
