Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(F_{đh}=k.\Delta l\Rightarrow k=\dfrac{F_{đh}}{\Delta l}=\dfrac{4,5}{0,15-0,12}=150\left(N/m\right)\)

Chọn D.
Độ biến dạng của lò xo là: Δl = l - l0 = 18 - 15 = 3 cm = 0,03 m
Lực kéo cân bằng với lực đàn hồi: Fk = Fđh = k.Δl
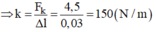

Độ dãn lò xo:
\(\Delta l=l-l_0=35-30=5cm=0,05m\)
Lực đàn hồi:
\(F_{đh}=k\cdot\Delta l\)
\(\Rightarrow k=\dfrac{F_{đh}}{\Delta l}=\dfrac{7,5}{0,05}=150\)N/m

a)Độ lớn của lực đàn hồi: \(F_{đh}=5N\)
b)Độ biến dạng của lò xo: \(\Delta l=\dfrac{F_{đh}}{k}=\dfrac{5}{100}=0,05m=5cm\)
c)Để lò xo dãn thêm 2cm tức \(\Delta l'=2+5=7cm=0,07m\)
Lực đàn hồi lúc này: \(F'_{đh}=0,07\cdot100=7N\)
Cần tăng lực kéo thêm: \(\Delta F=7-5=2N\)

Chọn đáp án C
Lò xo bị nén lại nên ℓo > ℓ
Áp dụng:
F = k∆ℓ = k(ℓo - ℓ)
→ 1 = 40(0,1 - ℓ)
→ ℓ = 0,075 m = 7,5 cm.
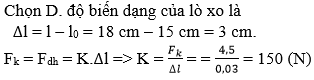
Ta có: \(F_{đh}=k.\Delta l\Rightarrow k=\dfrac{F_{đh}}{\Delta l}=\dfrac{4,5}{0,15-0,12}=150\left(N/m\right)\)