LT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 10 2022
Câu 2:
a: 0,(32)+0,(67)
=32/99+67/99
=1
b: \(0.\left(33\right)\cdot3=\dfrac{1}{3}\cdot3=1\)
TM
0
18 tháng 12 2015
|x - 4| + |6 - x| = 0
|x - 4| ; |6 - x| \(\ge\) 0
=> |x - 4| = |6 - x| = 0
|x - 4| = 0 => x= 4
|6 - x| = 0 => x= 6
Vì \(4\ne6\) n ê n không có giá trị của x
Bạn làm các câu khác tương tự
CC
1
15 tháng 11 2018
a) 0,(37)+0,(62) = 1
Có 0.(37)=\(\frac{37}{99}\)và 0.(62) = \(\frac{62}{99}\)
\(\frac{37}{99}\)+ \(\frac{62}{99}\)= 1
\(\Rightarrow0,\left(37\right)+0.\left(62\right)=1\)
b)\(0,\left(37\right)\times3=1\)
Có: \(0,\left(37\right)=\frac{37}{99}\)
\(\frac{37}{99}\times3=1\)
\(\Rightarrow0\left(37\right)\times3=1\)
H9
HT.Phong (9A5)
CTVHS
22 tháng 6 2023
\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{99}}\)
\(\Rightarrow\dfrac{A}{3}=\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{100}}\)
\(\Rightarrow A-\dfrac{A}{3}=\dfrac{2A}{3}=\left(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}\right)-\left(\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{100}}\right)\)
\(\Rightarrow\dfrac{2A}{3}=\left(\dfrac{1}{3^2}-\dfrac{1}{3^2}\right)+\left(\dfrac{1}{3^3}-\dfrac{1}{3^3}\right)+...+\left(\dfrac{1}{3^{99}}-\dfrac{1}{3^{99}}\right)+\left(\dfrac{1}{3}-\dfrac{1}{3^{100}}\right)=\dfrac{1}{3}-\dfrac{1}{3^{100}}\)
\(\Rightarrow2A=3\cdot\left(\dfrac{1}{3}-\dfrac{1}{3^{100}}\right)\)
\(\Rightarrow\text{A}=\dfrac{1-\dfrac{1}{3^{99}}}{2}\)
\(\Rightarrow A=\dfrac{1}{2}-\dfrac{1}{2.3^{99}}< \dfrac{1}{2}\)
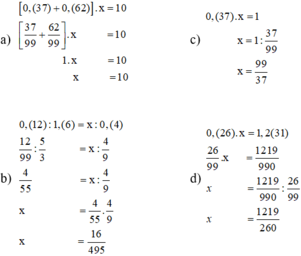
1)
a)\(0,\left(32\right)+0,\left(67\right)\)
\(=0,\left(01\right).32+0,\left(01\right).67\)
\(=0,\left(01\right).\left(32+67\right)\)
\(=\frac{1}{99}.99\)
\(=1\left(đpcm\right)\)
b)\(0,\left(33\right).3\)
\(=0,\left(01\right).33.3\)
\(=\frac{1}{99}.33.3\)
\(=\frac{33}{99}.3\)
\(=\frac{99}{99}\)
\(=1\left(đpcm\right)\)
2)\(0,\left(12\right):1,\left(6\right)=x:0,\left(3\right)\)
\(\left[\left(0,01\right).12\right]:\left[1+0,\left(6\right)\right]=x:\left[0,\left(1\right).3\right]\)
\(\left(\frac{1}{99}.12\right):\left[1+0,\left(1\right).6\right]=x:\left(\frac{1}{9}.3\right)\)
\(\frac{4}{33}:\left[1+\frac{1}{9}.6\right]=x:\frac{1}{3}\)
\(\frac{4}{33}:\left[1+\frac{2}{3}\right]=x.3\)
\(3x=\frac{4}{33}:\frac{5}{3}\)
\(3x=\frac{4}{33}\cdot\frac{3}{5}\)
\(3x=\frac{4}{55}\)
\(x=\frac{4}{55}:3\)
\(x=\frac{4}{55}\cdot\frac{1}{3}\)
\(x=\frac{4}{165}\)