Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đặt \(\frac{x}{4}=\frac{y}{7}=k\)
\(\Rightarrow x=4k;y=7k\)
Mà xy = 112
\(\Rightarrow\)4k . 7k = 112
28k2 = 112
k2 = 112 : 28
k2 = 4
k = 2 hoặc k = -2
với k = 2 thì : x = 8 ; y = 14
với k = -2 thì : x = -8 ; y = -14
Vậy ...
b) vì \(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}=\frac{a+b+c}{b+c+a}=1\)
\(\Rightarrow a=b;b=c;c=a\)
\(\Rightarrow a=b=c\)
3.
gọi số tờ tiền loại 2000đ , 5000đ , 10000đ lần lượt là a,b,c và a + b + c = 16
Theo bài ra : 2000a = 5000b = 10000c
\(\Rightarrow\frac{a}{5}=\frac{b}{2}=\frac{c}{1}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :
\(\frac{a}{5}=\frac{b}{2}=\frac{c}{1}=\frac{a+b+c}{5+2+1}=\frac{16}{8}=2\)
\(\Rightarrow a=10;b=4;c=2\)
Vậy có 10 tờ tiền 2000đ, 4 tờ tiền 5000đ, 2 tờ tiền 10000đ

Gọi a,b,c là tờ giấy bạc theo thứ tự 2000đ,5000đ và 10000đ.
Ta có a+b+c=16, 2000a=5000b = 10000c
Nhân mỗi vế vs 1/10000 để rút gọn
=> 2000a/10000=5000b/10000=10000c/10000
=> a/5=b/2=c/1
Vậy a/5+b/2+c/1 = a+b+c=5+2+1=16/8=2
Từ a/5=2=> a=2.5=10
b/2=2=> b=2.2=4
c/1=2=>c=1.2=2
Vậy số giấy bọc loại 2000đ là 10 tờ
số giấy bọc loại 5000đ là 4 tờ
số giấy bọc loại 10000đ là 2 tờ

Gọi a,b,c là số tờ tiền loại 2000đ,10000đ,5000đ. Ta có 2000a=10000b=5000c =>a/5=b/1=c/2 và a+b+c=16
Theo tính chất dãy tỉ số bằng nhau: a/5=b/1=c/2=a+b+c/5+1+2=16/8=2
=>a=2.5=10
b=2.1=2
c=2.2=4
Vậy có 10 tờ tiền loại 2000đ, 2 tờ tiền loại 10000đ, 4 tờ tiền loại 5000đ

Gọi x, y, z lần lượt là số tờ giấy bạc các loại 2000đ, 5000đ, và 10000đ (x; y; z ∈ N* và x; y; z < 16).
Có tất cả 16 tờ giấy bạc nên ta có: x + y + z = 16
2000.x = 5000.y = 10000.z
Suy ra: 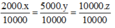
Hay 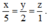
Theo tính chất dãy tỉ số bằng nhau ta có:
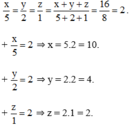
Vậy có 10 ờ loại 2000đ, 4 tờ loại 5000đ và 2 tờ loại 10000đ

rong các nhân vật Sơn Tinh , Thánh Gióng , Thạch sanh em thích nhân vật nào nhứt ! Vì SAO?
Nè ti k cần mấy người dạy đời nhé tui bị trừ điểm hay xóa nick là chuyện của tui
tui cần ấy người trả lời thui ai trả lời hay và nhanh tui k cho 3 cái nhé
tối nay hạn chót òi

Gọi tờ giấy bạc loại 2000đ, 5000đ, 10000đ theo thứ tự là x,y,z ( x,y,z \(\in\) N* )
Theo đề bài ra ta có :
\(x+y+z=16\) và \(2000x=5000y=10000z\)
Biến đổi : \(2000x=5000y=10000z\Rightarrow\frac{2000x}{10000}=\frac{5000y}{10000}=\frac{10000z}{10000}\)
\(\Rightarrow\frac{x}{5}=\frac{y}{2}=\frac{z}{1}\)
Theo tính chất của dãy tỉ số bằng nhau :
\(\frac{x}{5}=\frac{y}{2}=\frac{z}{1}=\frac{x+y+z}{5+2+1}=\frac{16}{8}=2\)
\(\Rightarrow x=2.5=10\)
\(y=2.2=4\)
\(z=2.1=2\)
Vậy số tờ bạc loại 2000đ,5000đ,10000đ theo thứ tự là 10;4;2

Gọi x, y, z lần lượt là số tờ giấy bạc loại 2000đ, 5000đ, 10000đ
Ta có: x + y + z = 16
2000x = 5000y = 10000z
Suy ra: 2000x10000=5000y10000=10000z100002000x10000=5000y10000=10000z10000
⇒x5=y2=z1⇒x5=y2=z1
Theo tính chất dãy tỉ số bằng nhau ta có:
x5=y2=z1=x+y+z5+2+1=168=2x5=y2=z1=x+y+z5+2+1=168=2
Ta có:
x5=2⇒x=5.2=10x5=2⇒x=5.2=10
y2=2⇒y=2.2=4y2=2⇒y=2.2=4
z1=2⇒z=2.1=2z1=2⇒z=2.1=2
Vậy có 10 tờ loại 2000đ, 4 tờ loại 5000đ, 2 tờ loại 10000đ
Gọi số tờ tiền loại 2 000 đồng là a, 5000 đồng là c, 10 000 đồng là b. (a+b+c)=16
Ta có: a.2000 = b.10000 = c.5000
\(\Rightarrow a\div\frac{1}{2000}=b\div\frac{1}{10000}=c\div\frac{1}{5000}\)
\(\Rightarrow\frac{a}{\frac{1}{2000}}=\frac{b}{\frac{1}{10000}}=\frac{c}{\frac{1}{5000}}\)
Áp dụng tình chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{\frac{1}{2000}}=\frac{b}{\frac{1}{10000}}=\frac{c}{\frac{1}{5000}}=\frac{a+b+c}{\frac{1}{2000}+\frac{1}{10000}+\frac{1}{5000}}=\frac{16}{\frac{1}{1250}}=20000\)
\(\Rightarrow\frac{a}{\frac{1}{2000}}=20000\Rightarrow a=20000\times\frac{1}{2000}=10\)
\(\Rightarrow\frac{b}{\frac{1}{10000}}=20000\Rightarrow b=20000\times\frac{1}{10000}=2\)
\(\frac{c}{\frac{1}{5000}}=20000\Rightarrow c=20000\times\frac{1}{5000}=4\)
Vậy có 10 tờ 2000đ, 2 tờ 10000đ, 4 tờ 5000đ
1. \(\frac{x}{4}=\frac{y}{7}\)và \(xy=112\)
đặt \(\frac{x}{4}=\frac{y}{7}=k\)
\(\Rightarrow x=4k;y=7k\)
ta có:\(xy=4k\cdot7k=28k^2=112\)
\(\Rightarrow k^2=112:28=4\)
\(\Rightarrow\orbr{\begin{cases}k=2\\k=-2\end{cases}}\)
TH1: \(\hept{\begin{cases}x=2\cdot4=8\\y=2\cdot7=14\end{cases}}\)
TH2: \(\hept{\begin{cases}x=-2\cdot4=-8\\y=-2\cdot7=-14\end{cases}}\)