Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
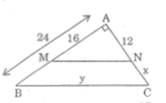
Trong ΔABC, ta có: MN // BC (gt)
Suy ra: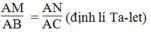 
Suy ra: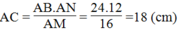 
Vậy NC = AC – AN = 18 – 12 = 6(cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông AMN, ta có:
M N 2 = A M 2 + A N 2 = 16 2 + 12 2 = 400
MN = 20cm
Trong ΔABC, ta có: MN // BC (gt)
Suy ra:
Vậy: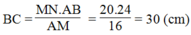
Ta có: MN // BC (gt), áp dụng hệ quả của định lý Ta – lét suy ra:
Suy ra: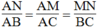 
(Hệ quả định lí Ta-lét)
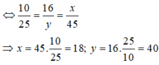
Hình bạn tự vẽ nhé
Áp dụng định lý Pi-ta-go vào tam giác AMN vuông tại A ta được:
\(AM^2+AN^2=MN^2\)
\(400=MN^2\)
\(\Rightarrow MN=20\)
Xét tam giác AMN có BC//MN
\(\Rightarrow\frac{AM}{AB}=\frac{MN}{BC}=\frac{AN}{AC}\)( Hệ qua của định lý Ta-let)
\(\Rightarrow\frac{2}{3}=\frac{20}{BC}=\frac{12}{AC}\)
\(\Rightarrow\hept{\begin{cases}BC=30\left(cm\right)\\AC=18\left(cm\right)\end{cases}}\)
Ta có: AN+NC=AC ( h.vẽ)
\(\Rightarrow NC=6\)(cm)
Vậy ...
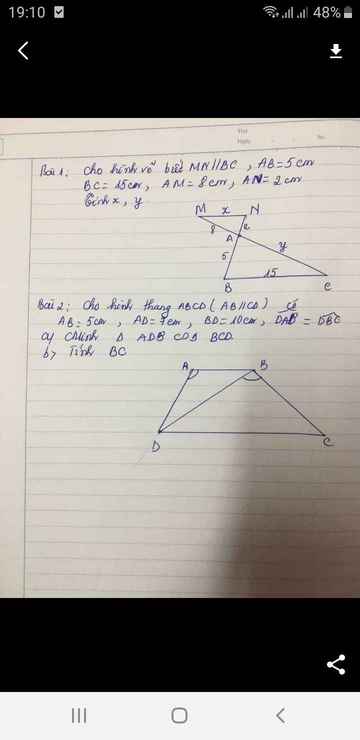
Xét ΔACB có MN//BC
nên AN/AB=AM/AC
=>AM/35=2/5
=>AM=14cm
MN//BC
=>MN/BC=AN/AB=2/5
=>16/BC=2/5
=>BC=40cm
a) Do MN//BC nên theo hệ quả của ĐL Ta-let ta có \(\dfrac{AM}{AB}\)=\(\dfrac{MN}{BC}\)
\(\Rightarrow\) \(\dfrac{2}{4}\) = \(\dfrac{MN}{6}\)\(\Rightarrow\) MN = \(\dfrac{2\times6}{4}\)\(\Rightarrow\) MN = 3 cm
b) Do MN//BC nên theo ĐL Ta-let ta có \(\dfrac{AM}{AB}\)=\(\dfrac{AN}{AC}\)
\(\Rightarrow\)\(\dfrac{12}{15}\)=\(\dfrac{AN}{18}\)\(\Rightarrow\) AN = \(\dfrac{12\times18}{15}\) = 14,4 cm
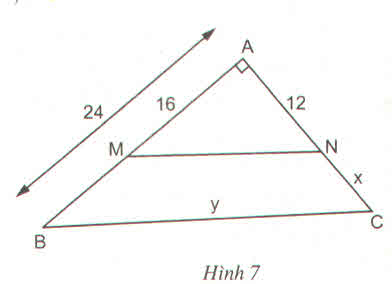
\(\Delta ABC\) có \(MN//BC\) áp dụng định lý Ta-lét ta có:
\(\frac{AM}{AB}=\frac{AN}{AC}\)
hay \(\frac{16}{24}=\frac{12}{AC}=\frac{MN}{BC}\)
\(\Rightarrow\)\(AC=\frac{24.12}{16}=18\) cm
Áp dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\)\(BC^2=24^2+18^2=900\)
\(\Leftrightarrow\)\(BC=\sqrt{900}=30\)cm
Áp dụng định lí Ta-lét ta có:
\(\frac{MN}{BC}=\frac{AN}{AC}=\frac{AM}{AB}\Leftrightarrow\frac{MN}{BC}=\frac{12}{AC}=\frac{16}{24}=\frac{2}{3}\)
\(\Rightarrow\frac{12}{AC}=\frac{2}{3}\Leftrightarrow2AC=36\Leftrightarrow AC=18\left(cm\right)\)
\(AC=AN+NC\Leftrightarrow18=12+NC\Rightarrow NC=6\left(cm\right)\)
\(\text{ }\text{Áp dụng định lí Py-ta-go vào tam giác vuông ABC ta có:}\)
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow24^2+18^2=BC^2\)
\(\Leftrightarrow BC^2=900\Rightarrow BC=30\left(cm\right)\)
Vậy....
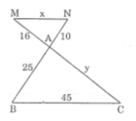
a; Xét ΔBAC có MN//BC
nên AM/AB=AN/AC
=>AM/20=15/20
=>AM=15
b: Xét ΔABC có MN//BC
nên AN/NC=AM/MB
=>AN/NC=3/2
=>AN/3=NC/2
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AN}{3}=\dfrac{NC}{2}=\dfrac{AN+NC}{3+2}=\dfrac{5}{5}=1\)
Do đó: NC=2
c: Xét ΔBCA có MN//BC
nên MN/BC=AM/AB
=>MN/6=8/12=2/3
hay MN=4
