Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Xét tứ giác ABCD có
AB//CD
AB=CD
Do đó:ABCD là hình bình hành
Suy ra: AD=BC

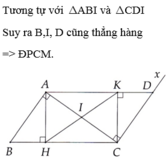
1) Ta có hình vẽ sau:
Vì AB // CD nên \(\widehat{A_1}\) = \(\widehat{C_1}\) (so le trong)
AD // BC nên \(\widehat{A_2}\) = \(\widehat{C_2}\) ( so le trong)
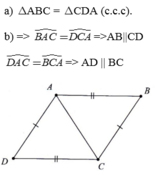
Xét ΔABC và ΔCDA có:
\(\widehat{A_1}\) = \(\widehat{C_1}\) (cm trên)
AC: Cạnh chung
\(\widehat{A_2}\) = \(\widehat{C_2}\) (cm trên)
\(\Rightarrow\) ΔABC = ΔCDA (g.c.g) (đpcm)
2) Chứng minh tương tự ta có: ΔCDA = ABC (g.c.g)
\(\Rightarrow\) AB = CD ( 2 cạnh tương ứng) (đpcm)
3) Mình sửa lại chỗ AE = AC là AE = AB đó nha, bn ghi nhầm đề!!!
Ta có hình vẽ sau:
Xét ΔABC và ΔAFE có:
AE = AB (gt)
\(\widehat{A_1}\) = \(\widehat{A_2}\) (đối đỉnh)
AF = AC (gt)
\(\Rightarrow\) ΔABC = ΔAFE(c.g.c) (đpcm)
Bạn áp dụng trường hợp bằng nhau cạnh - góc - cạnh của tam giác rồi chứng minh nha

ta có : AB//CD và AD//BC
=> ABCD là hình bình hành
=>theo tính chất hình bình hành thì AB=CD VÀ BD = AD
B) nếu O là giao hai đường chéo thì mới làm dduocj
theo tính chất hình bình hành thì hai đường chéo giao nhau tại trung điểm mỗi đường
=> OC=OA và OB=OD

\(a,\left\{{}\begin{matrix}BM=MC\\AM=MD\\\widehat{AMB}=\widehat{CMD}\left(đđ\right)\end{matrix}\right.\Rightarrow\Delta MAB=\Delta MDC\left(c.g.c\right)\\ b,\Delta MAB=\Delta MDC\\ \Rightarrow\widehat{MCD}=\widehat{MBA}\)
Mà 2 góc này ở vị trí so le trong nên \(AB\text{//}CD\)
\(c,\left\{{}\begin{matrix}BM=MC\\AM=MD\\\widehat{AMC}=\widehat{BMD}\left(đđ\right)\end{matrix}\right.\Rightarrow\Delta MAC=\Delta MDB\left(c.g.c\right)\\ \Rightarrow AC=BD;\widehat{MCA}=\widehat{MBD}\)
Mà 2 góc này ở vị trí slt nên \(AC\text{//}BD\Rightarrow BD\bot AB\)
\(\left\{{}\begin{matrix}AC=BD\\\widehat{BAC}=\widehat{ABD}=90^0\\AB\text{ chung}\end{matrix}\right.\Rightarrow\Delta ABC=\Delta CDA\left(c.g.c\right)\\ \Rightarrow BC=AD\\ d,MF\bot BD\Rightarrow MF\text{//}AB\\ BC=AD\\ \Rightarrow AM=\dfrac{1}{2}AD=\dfrac{1}{2}BC=BM=MC\\ \Rightarrow\Delta AME\text{ cân tại }E\)
Mà ME là trung tuyến nên cũng là đường cao
Do đó \(ME\bot AC\Rightarrow ME\text{//}AB\)
Mà \(MF\text{//}AB\Rightarrow ME\equiv MF\)
Vậy M,E,F thẳng hàng


 Cho hình vẽ A B
Cho hình vẽ A B
mk ko thấy hình ảnh bạn ơi
mình đã đăng lại rồi nhé