Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác BMDN có
BN//DM
BN=DM
Do đó: BMDN là hình bình hành
Suy ra: BM//DN
b: Ta có: ABCD là hình chữ nhật
nên AC cắt BD tại trung điểm của mỗi đường
hay O là trung điểm chung của AC và BD(1)
Ta có: BMDN là hình bình hành
nên BD cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của BD
nên O là trung điểm của MN(2)
Từ (1) và (2) suy ra AC,BD,MN đồng quy

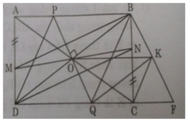
b) O là trung điểm của BD mà ABCD là hình chữ nhật nên đường chéo thứ hai AC phải qua O.
Lại có tứ giác BMDN là hình bình hành nên MN phải đi qua trung điểm O của BD.
Vậy AC, BD, MN đồng quy tại O.

1:
a: Xét tứ giác BMDN có
DM//BN
DM=BN
Do đó: BMDN là hình bình hành
Suy ra: BM//DN

Hình em tự kẻ nhé .
a)Vì \(ABCD\)là hcn
\(\Rightarrow\hept{\begin{cases}AD//BC\\AD=BC\end{cases}}\)
mà \(AM=CN\)
\(\Rightarrow AD-AM=BC-CN\)
hay \(DM=BN\)
Xét tứ giác BNDM ,có:
\(\hept{\begin{cases}DM=BN\\DM//BN\end{cases}}\)
\(\Rightarrow BNDM\)là hình bình hành
\(\Rightarrow BM//DN\)
b) //Đề sai nhé , O là trung điểm của BD thì AC,BD,MN mới đồng quy tại O được .
Vì BNDM là hình bình hành
và O là trung điểm của BD
\(\Rightarrow O\)là trung điểm của MN
Ta có : ABCD là hcn
O là trung điểm của BD
\(\Rightarrow O\)là trung điểm của AC
Suy ra : AC,BD,MN đồng quy tại O

Gọi O là giao điểm 2 đường chéo AC và BD
Xét \(\Delta\)AOE và \(\Delta\)COF có:AO=OC ( vì ABCD là hình bình hành ),CF=AE ( giả thiết ),^AOE=^COF ( đối đỉnh )
a
Vì vậy \(\Delta AOE=\Delta COF\left(c.g.c\right)\Rightarrow OE=OF\left(1\right)\)
Xét \(\Delta\)BON và \(\Delta\)DOM có:OB=OD ( vì ABCD là hình bình hành ),MD=BN ( vì AM=CN ),^MOD=^NOB ( đối đỉnh )
Vì vậy \(\Delta BON=\Delta COM\left(c.g.c\right)\Rightarrow OM=ON\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\) suy ra tứ giác EMFN là hình bình hành.
b
Hình bình hành EMFN có O là giao điểm của 2 đường chéo,tứ giác ABCD có O là giao điểm của 2 đường chéo.
=> ĐPCM
P/S:Mik ko chắc lắm đâu nha,nhất là câu b ý:p

a: Xét tứ giác BMDN có
BN//DM
BN=DM
Do đó: BMDN là hình bình hành
=>BM//DN và BD cắt MN tại trung điểm của mỗi đường(1)
b: Vì ABCD là hình bình hành
nên AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1)va (2) suy ra AC,BD,MN đồng quy tại O
a: Xét tứ giác BMDN có
BN//DM
BN=DM
Do đó: BMDN là hình bình hành
Suy ra: BM//DN
b: Ta có: BMDN là hình bình hành
nên BD cắt MN tại trung điểm của mỗi đường(1)
Ta có: ABCD là hình bình hành
nên AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra BD,MN,AC đồng quy