Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(1\)) \(5-\left(10-x\right)=7\)
\(10-x=5-7\)
\(10-x=-2\)
\(x=10-\left(-2\right)\)
\(x=12\)
\(2\)) \(-32-\left(x-5\right)=0\)
\(x-5=-32-0\)
\(x-5=-32\)
\(x=-32+5\)
\(x=-27\)

Hai bài bị trùng nhau nên các bạn nhìn ảnh hay văn bản đều như nhau ạ
c: =>x+2>0
hay x>-2
d: =>-4<=x<=3
e: =>\(x\in\varnothing\)
f: \(\Leftrightarrow\left[{}\begin{matrix}x>4\\x< -6\end{matrix}\right.\)

1) Ta có: \(3\left(x-1\right)-5\left(x-2\right)=4\left(x+1\right)\)
\(\Leftrightarrow3x-5-5x+10-4x-4=0\)
\(\Leftrightarrow-6x+1=0\)
\(\Leftrightarrow-6x=-1\)
hay \(x=\dfrac{1}{6}\)
2) Ta có: \(-2\left(x-2\right)-4\left(x+1\right)=-3\left(x+3\right)\)
\(\Leftrightarrow-2x+4-4x-4+3x+9=0\)
\(\Leftrightarrow-3x=-9\)
hay x=3
3) Ta có: \(3x^2+2x=0\)
\(\Leftrightarrow x\left(3x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{2}{3}\end{matrix}\right.\)
4) Ta có: \(x^2-5x=0\)
\(\Leftrightarrow x\left(x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)
5) Ta có: \(\left(2x-3\right)^2=36\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=6\\2x-3=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=9\\2x=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{9}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)
6) Ta có: \(\left(5x-1\right)^3=125\)
\(\Leftrightarrow5x-1=5\)
\(\Leftrightarrow5x=6\)
hay \(x=\dfrac{6}{5}\)
7) Ta có: \(3^{x+1}=27\)
\(\Leftrightarrow x+1=3\)
hay x=2

1:
=>2x-3=0 hoặc 5/2-x=0
=>x=3/2 hoặc x=5/2
2: =>x=1/2+12=12,5
3: =>(2x+3/5-3/5)(2x+3/5+3/5)=0
=>2x(2x+6/5)=0
=>x=0 hoặc x=-3/5
4: =>-1/6x=-1/3
=>x=1/3:1/6=2
5: =>1/4:x=1/4
=>x=1
6: =>2/5x+11/15=1
=>2/5x=4/15
=>x=2/3

1) Ta có: \(\left(-5+x\right)\left(x-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-5+x=0\\x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=7\end{matrix}\right.\)
Vậy: \(x\in\left\{5;7\right\}\)
2) Ta có: \(\left(30-x\right)\left(2x-16\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}30-x=0\\2x-16=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-x=-30\\2x=16\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=30\\x=8\end{matrix}\right.\)
Vậy: \(x\in\left\{30;8\right\}\)
3) Ta có: \(\left(-5-x\right)\left(17+x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-5-x=0\\17+x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-x=5\\x=0-17\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-17\end{matrix}\right.\)
Vậy: \(x\in\left\{-5;-17\right\}\)
4) Ta có: \(\left(-3x+18\right)\left(-5x-10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-3x+18=0\\-5x-10=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-3x=-18\\-5x=10\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\)
Vậy: \(x\in\left\{6;-2\right\}\)
Bài nay ta có hai vế bạn hãy đặt giả sử một trong hai vế bằng 0 rồi giải phương trình cho mỗi vế bằng o

TH1: x3+1 = 0 => x3 = 0-1 = -1 => x= -1:3 ko được => x ko có giá trị
TH2: x2+4 = 0=> x2 = 0-4 = -4 => x= -4:2 = -2
TH3: x-1 = 0 => x= 0+1 = 1
duyệt đi

l) (x + 9) . (x2 – 25) = 0
<=> (x + 9) . (x – 5) . (x + 5) = 0
<=> \(\left[{}\begin{matrix}\text{x + 9 = 0}\\x-5=0\\x+5=0\end{matrix}\right.\left[{}\begin{matrix}x=-9\\x=5\\x=-5\end{matrix}\right.\)
Vậy S = \(\left\{-9,5,-5\right\}\)
e) |x - 4 |< 7
<=> \(\left[{}\begin{matrix}x-4=7\\x-4=-7\end{matrix}\right.< =>\left[{}\begin{matrix}x=11\\x=-3\end{matrix}\right.\)
Vậy S = \(\left\{11;-3\right\}\)
I,(x+9).(x^2-25)=0
tương đương:x+9=0
x^2-25=0
tương đương : x=-9
x=5
e,\(\left|x-4\right|\)=7
tương đương x-4=4
x-4=-4
tương đương :x=0
x=-8
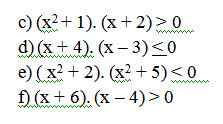 Giúp mình với, mình cần gấp ạ
Giúp mình với, mình cần gấp ạ
Ta có : \(\left(3-x\right)\left|x+5\right|=0\)
\(\Leftrightarrow\orbr{\begin{cases}3-x=0\\\left|x+5\right|=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=3\\x+5=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=3\\x=-5\end{cases}}\)
Ta có :
\(\left(3-x\right)\left|x+5\right|=0\)
\(\Rightarrow\orbr{\begin{cases}3-x=0\\\left|x+5\right|=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=3\\x+5=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=3\\x=-5\end{cases}}\)