Bài 1: Cho tam giác ABC, các tia phân giác của góc B, C cắt nhau tại I
a) Trong tam giác BIC, cạnh nào là cạnh lớn nhất?
b) Nếu có IB < IC, hãy so sánh cạnh AB và AC
Bài 2: Cho tam giác ABC đều. Điểm M thuộc cạnh BC sao cho BM = \(\dfrac{1}{3}\)BC. Gọi N là trung điểm của MC
a) Chứng minh △ABM = △CAN
b) So sánh AB và AN
c) Trên tia đối của AM lấy điểm D sao cho M là trung điểm của AD. So sánh \(\widehat{DAN}\) và \(\widehat{ADN}\)
d) Chứng minh rằng \(\widehat{BAM}\) < \(20^{o}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo định lí tổng ba góc của một tam giác bằng 180 độ: Xét trong tam giác ABC, ta có:
\(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^o\Rightarrow\widehat{ABC}+\widehat{ACB}=180^o-\widehat{BAC}\)(1)
Vì BI là phân giác \(\widehat{ABC}\Rightarrow\widehat{IBC}=\frac{1}{2}\widehat{ABC}\)
CI là phân giác \(\widehat{ACB}\Rightarrow\widehat{ICB}=\frac{1}{2}\widehat{ACB}\)
Xét trong tam giác ICB có: \(\widehat{BIC}+\widehat{IBC}+\widehat{ICB}=180^o\Rightarrow\widehat{BIC}=180^o-\widehat{IBC}-\widehat{ICB}=180^o-\frac{1}{2}\left(\widehat{ABC}+\widehat{ACB}\right)\)(2)
Từ (1), (2) => \(\widehat{BIC}=180^o-\frac{1}{2}\left(180^o-\widehat{BAC}\right)=90^o+\widehat{BAC}>90^o\)
=> góc BIC là góc tù cũng là góc lớn nhất=> Cạnh BC đối diện góc BIC là cạnh lớn nhất trong tam giác BIC
b) Giả sử IB<IC => \(\widehat{ICB}< \widehat{IBC}\Rightarrow\widehat{ACB}< \widehat{ABC}\Rightarrow AB< AC\)

k bạn ơi, giải giúp mik câu c đi bạn. mik giải đc 2 câu trên r

a) Xét trong tam giác BIC từ định lí tổng 3 góc của một tam giác bằng 10 độ
=> \(\widehat{BIC}=180^o-\widehat{IBC}-\widehat{ICB}\)\(=180^o-\frac{1}{2}\widehat{ABC}-\frac{1}{2}\widehat{ACB}\)( tính chất phân giác)
\(=180^o-\frac{1}{2}\left(\widehat{ABC}+\widehat{ACB}\right)\)
Mà xét trong tam giác ABC cũng từ định lí tổng ba góc của một tam giác bằng 180 độ
=> \(\widehat{ABC}+\widehat{ACB}=180^o-\widehat{BCA}=180^o-60^o=120^o\)
=> \(\widehat{BIC}=180^o-\frac{1}{2}.120^o=120^o\)
b) Xét tam giác BEI và tam giác BFI
Hai tam giác này bằng nhau theo trường hợp góc cạnh góc (tự chứng minh)
=> \(\widehat{EIB}=\widehat{FIB}\)
Mà \(\widehat{EIB}=\widehat{DIC}=180^o-\widehat{BIC}=60^o\)
=> \(\widehat{BIF}=60^o\Rightarrow\widehat{CIF}=\widehat{BIC}-\widehat{BIF}=120^o-60^o=60^o\)
=> \(\widehat{CID}=\widehat{CIF}\)
Xét Tam giác IDC và tam giác IFC có:
IC chung
\(\widehat{CID}=\widehat{CIF}\)
\(\widehat{FIC}=\widehat{DIC}\)
=> \(\Delta CID=\Delta CIF\)(g-c-g)
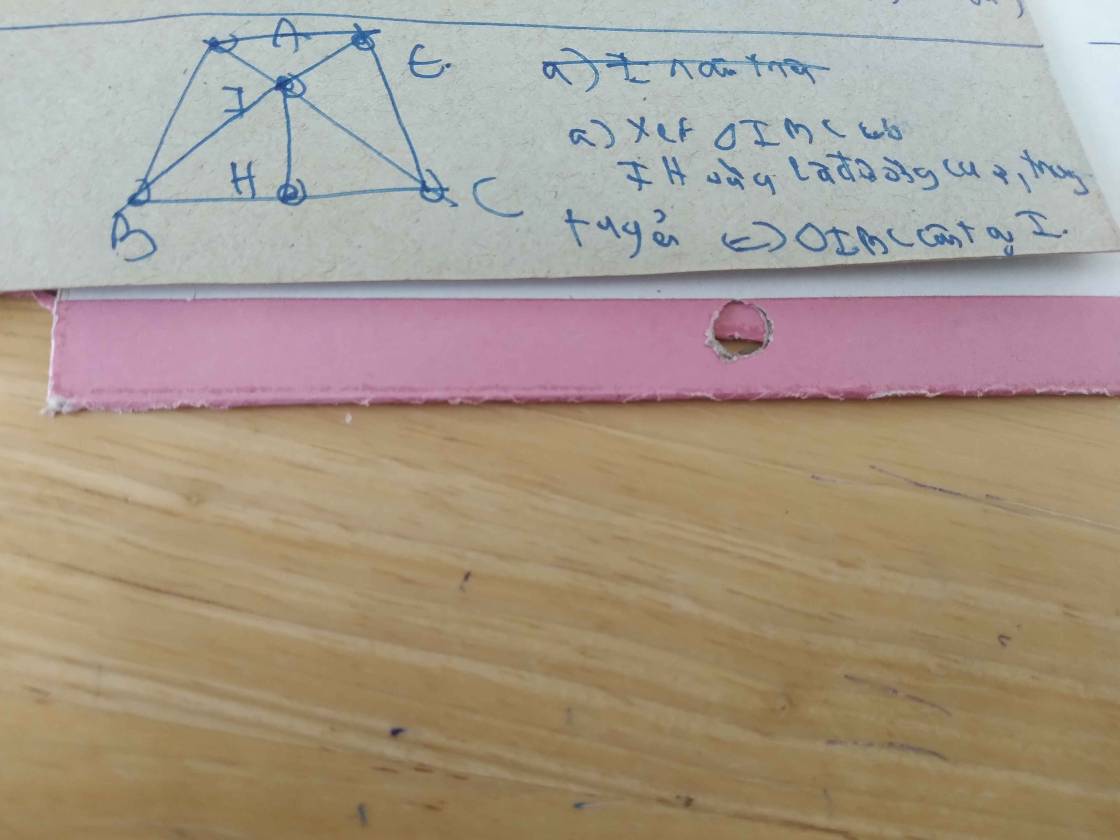

Bài 2: Em tham khảo bài tương tự tại đây nhé.
Câu hỏi của Dang Khanh Ngoc - Toán lớp 7 - Học toán với OnlineMath
Bài 1 ai lm ik cho mk tham khảo nữa