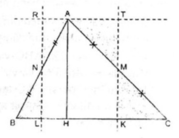
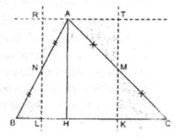
CMR: Nếu 1 đường thẳng chia chu vi và diện tích của tam giác thành 2 phần bằng nhau thì đường thẳng đó đi qua giao điểm 3 đường phân giác của tam giác đó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


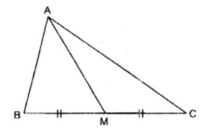
Ta đã biết hai tam giác có cạnh đáy bằng nhau và chung chiều cao thì có diện tích bằng nhau. Giả sử △ ABC. Gọi M là trung điểm của BC
Cắt tam giác ABC theo đường AM chia tam giác ABC ra hai phần có diện tích bằng nhau.

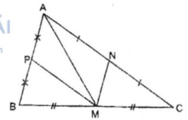
Tương tự như trên câu b.
Xét Δ ABC. Gọi M là trung điểm của BC
N là trung điểm của AC, P là trung điểm của AB
Cắt tam giác ABC theo đường AM ta có hai phần có diện tích bằng nhau
Cắt tam giác AMC theo đường AN ta có hai phần có diện tích bằng nhau
Cắt tam giác AMB theo đường MP ta có hai phần diện tích bằng nhau, ta có diện tích bốn phần chia bằng nhau.

TA DỰNG NHƯ HÌNH VẼ
ĐẶT S ORQ = n^2 , S OMP = n^2+1 , S OSN = n^2+3
DỄ DÀNG NHẬN THẤY:
TAM GIÁC ORQ ĐỒNG DẠNG VỚI TAM GIÁC PMO
=> \(\frac{OQ}{OP}=\frac{\pi}{\sqrt{\pi^2+1}}\)
=> \(\frac{OQ}{PQ}=\frac{\pi}{\sqrt{\pi^2+1}+\pi}\)
=> S ORQ = \(\frac{\pi^2}{\left(\sqrt{\pi^2+1}+\pi\right)^2}SPQB\)
=> S PQB = \(\left(\sqrt[]{\pi^2+1}+\pi\right)^2\)
CHỨNG MINH TƯƠNG TỰ VỚI SAMN VÀ S SRC RỒI CỘNG LẠI TRỪ ĐI 2 LẦN TỔNG CỦA 3 TAM GIÁC TRONG ĐỀ BÀI LÀ RA DIỆN TÍCH TAM GIÁC ABC

Giả sử BM<MC khi đó: S(AMB)<S(AMC) Đặt I là trung điểm BC. Nối AM, AI. Qua I kẻ đường thẳng song song với AM và cắt AC tại N và AI giao với MN tại O. Đường thẳng MN chính là đường thẳng cần phải vẽ. Thật vây, tứ giác ANIM là hình thang nên S(AON)=S(MOI) Mặt khác: S(AIC)=1/2S(ABC)=S(AON)+S(CION)=S(MOI)+S(CION)=S(CMN)

Giả sử BM<MC khi đó: S(AMB)<S(AMC)
Đặt I là trung điểm BC. Nối AM, AI. Qua I kẻ đường thẳng song song với AM và cắt AC tại N và AI giao với MN tại O.
Đường thẳng MN chính là đường thẳng cần phải vẽ.
Thật vây, tứ giác ANIM là hình thang nên S(AON)=S(MOI)
Mặt khác:
S(AIC)=1/2S(ABC)=S(AON)+S(CION)=S(MOI)+S(CION)=S(CMN)