Đề: 1 tháp đồng hồ có đáy là hình vuông cạnh 5m, 1 phần là hình hộp chữ nhật cạnh là 12m, 1 phần là hình chóp đều, các mặt bên là các tam giác cân có cạnh bên là 8m. a). Tính chiều cao của tháp (làm tròn đến số thập phân thứ nhất)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 3 2017
Giả sử các kim tự tháp là hình chóp tứ giác đều S.ABCD.
Áp dụng định lí Pi-ta-go vào tam giác vuông AOB, ta có:
O A 2 + O B 2 = A B 2
Suy ra: 2. O A 2 = A B 2
Suy ra: O A 2 = A B 2 / 2 = 27144,5
Áp dụng định lí Pi-ta-go vào tam giác vuông SOA, ta có:
S A 2 = S O 2 + O A 2 =146,52 + 27144,5 = 48606,75
SA = 48606 , 75 ≈ 220,5(cm)
Kẻ SK ⊥ BC
Ta có: BK= KC = 1/2 BC = 116,5(m)
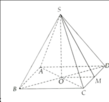
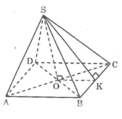
Kẻ trung tuyến SM của \(\bigtriangleup{SBC}\)
⇒BC=2MC=2MB
⇔MC=MB=\(\dfrac{5}{2}\)=2,5m
SMSM là trung tuyến ⇒SM⊥BC
Áp dụng định lý Pitago vào ΔSCM vuông tại M taΔSCM⊥M có:
\(SM =\)\(\sqrt{SC^2-CM^2} \) = \(\sqrt{8^2-2,5^2}\)= \(\dfrac{\sqrt{231}}{2}\) m
HM=\(\dfrac{1}{2}\).AB=2,5m
ΔSHM⊥H:HS= \(\sqrt{SM^2-HM^2} =\sqrt{\dfrac{231}{4}-2,5^2} =\dfrac{\sqrt{206}}{2}\)
Chiều cao của tháp là:
\(\dfrac{\sqrt{206}}{2} +12\) \(≈ \) \(19,2m\)