Tìm các số tự nhiên x thỏa mãn 10000<x< 15000. Và khi chia x cho 393 cũng như 655 đều có số dư 210?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 7 2018
a) ta có: 7x7 = 0
49x = 0
=> x = 0
=> A = {0}
b) ta có: 0.x = 0
mà x là số tự nhiên
=> x thuộc N
=> B = { x thuộc N}
c) ta có: x + 2 = x - 2
=> x - x = - 2 - 2
\(\Rightarrow x\in\varnothing\)
\(\Rightarrow C=\left\{\varnothing\right\}\)
DD
1
27 tháng 3 2023
=>x<11/10+67/30-7/60
=>x<66/60+134/60-7/60=193/60
mà x tự nhiên
nên \(x\in\left\{0;1;2;3\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 3 2022
Xét trên tập số tự nhiên
- Với \(y=0\Rightarrow\) ko tồn tại x thỏa mãn
- Với \(y=1\Rightarrow\) ko tồn tại x thỏa mãn
- Với \(y=2\Rightarrow x=1\)
- Với \(y\ge2\Rightarrow2^y⋮8\)
\(\Rightarrow5^x-1⋮8\)
Nếu \(x\) lẻ \(\Rightarrow x=2k+1\Rightarrow5^x=5.25^k\equiv5\left(mod8\right)\) \(\Rightarrow5^x-1\equiv4\left(mod8\right)\) ko chia hết cho 8 (ktm)
\(\Rightarrow x\) chẵn \(\Rightarrow x=2k\)
\(\Rightarrow5^x=5^{2k}=25^k\equiv1\left(mod3\right)\)
\(\Rightarrow5^x-1\equiv0\left(mod3\right)\Rightarrow5^x-1⋮3\Rightarrow2^y⋮3\) (vô lý)
Vậy với \(y\ge3\) ko tồn tại x;y thỏa mãn
Có đúng 1 cặp thỏa mãn là \(\left(x;y\right)=\left(1;2\right)\)
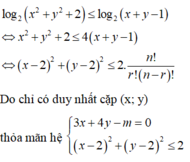
mk cho bài kham khảo nha :
a, (2n+7)/(n+1)=(2(n+1)+5)/(n+1)=2+5/(n+1)
Để (2n+7) chia hết (n+1) thì 5 chia hết cho n+1 hay n+1 là ước của 5
=>n+1 € {-5, -1 ,1, 5}
=>n € {-6,-2, 0,4}
Do n là STN=> n €{0,4}
b , n+2 chia hết cho (7-n) =>(n+2)(2-n) chia hết cho (7-n)
hay 4-n^2 chia hết cho 7-n => (4-n^2)/(7-n)=(49-n^2-45)/(7-n)
=>((7-n)(7+n)-45)/(7-n)=(7+n)-45/(7-n)
(n+2) chia hết (7-n) thì 45 chia hết cho (7-n)
=>7-n € {-45 ,-9, -5,-3,-15,-1,1,3,9,15,45}
=>n € {52,16,12,20,8,6,4,-2,-8,-38}
Do n là STN => n €{4,6,8,12,16,20,52}
:D