Cho hàm số y=(m2-2m+3)x-4 (d),(với m là tham số)
1.Chứng minh rằng với mọi m hàm số luôn đồng biến trên tập xác định của nó.
2. Tìm m để (d) đi qua A(2;8).
3. Tìm m để (d) song song với đường thẳng (d’): y=3x+m-4.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2) Để (d) đi qua A(2;8) thì Thay x=2 và y=8 vào hàm số \(y=\left(m^2-2m+3\right)x-4\), ta được:
\(\left(m^2-2m+3\right)\cdot2-4=8\)
\(\Leftrightarrow2m^2-4m+6-4-8=0\)
\(\Leftrightarrow2m^2-4m-6=0\)
\(\Leftrightarrow2m^2-6m+2m-6=0\)
\(\Leftrightarrow2m\left(m-3\right)+2\left(m-3\right)=0\)
\(\Leftrightarrow\left(m-3\right)\left(2m+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m-3=0\\2m+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=3\\2m=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=3\\m=-1\end{matrix}\right.\)
Vậy: Để (d) đi qua A(2;8) thì \(m\in\left\{3;-1\right\}\)

Với mọi tham số m ta có :
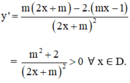
Vậy hàm số luôn đồng biến trên mỗi khoảng xác định của nó.

\(y=\dfrac{x^2-m^2+2m+1}{x-m}\) đúng không nhỉ?
\(y'=\dfrac{x^2-2mx+m^2-2m-1}{\left(x-m\right)^2}\)
Hàm đồng biến trên các khoảng xác định khi và chỉ khi:
\(x^2-2mx+m^2-2m-1\ge0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=m^2-\left(m^2-2m-1\right)\le0\)
\(\Leftrightarrow m\le-\dfrac{1}{2}\)

Đáp án A
T X D : D = ℝ \ 1
Ta có: y = m x 2 − m + 2 x + m 2 − 2 m + 2 x − 1 = m x − 2 + m 2 − 2 m x − 1 ⇒ y ' = m − m 2 − 2 m x − 1 2
hàm số luôn đồng biến trên tập xác định của nó khi y ' ≥ 0 ∀ x ∈ D (dấu bằng xảy ra tại hữu hạn điểm)
⇔ m − m 2 − 2 m x − 1 2 ≥ 0 ∀ x ∈ D ⇔ x x − 1 2 ≥ m 2 − 2 m ∀ x ∈ D
Với m = 0 ⇒ y ' = 0 ∀ x ∈ D (không thỏa mãn dấu bằng xảy ra tại hữu hạn điểm)
Khi đó hàm số luôn đồng biến trên tập xác định m > 0 m 2 − 2 m ≤ 0 ⇔ 0 < m ≤ 2
1. Xét : m^2-2m+3 = (m^2-2m+1)+2 = (m-1)^2+2 > 0
=> hàm số trên luôn đồng biến trên tập xác định của nó
2. Để (d) đi qua A(2;8) thì :
8 = (m^2-2m+3).2 - 4
=> m=3 hoặc m=-1
3. Để (d) // (d') : y=3x+m-4 thì : m^2-2m+3=3 và -4 khác m-4
=> m=0 hoặc m=2 và m khác 0 => m=2
Tk mk nha