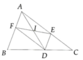
Cho tam giác ABC cân tại A từ điểm D trên BC kẻ đường thẳng song song với AB cắt AC ở E kẻ đường thẳng song song với AC cắt AB ở F dựng H đối xứng với D qua EF
a) Chứng minh tam giác BHF cân
b) Tứ giác AHFE là hình thang cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi Q là giao điểm của HD và FE
Xét tam giác FHD ta có:
FQ là đcao(D đối xứng với H qua FE)
FQ là đg trung tuyến HD(D đối xứng với H qua FE;Q là giao điểm của HD và FE)
=> tam giác FHD cân tại F
Ta có:
\(\widehat{ABC}=\widehat{ACB}\) (tam giác ABC cân tại A)
\(\widehat{ABC}=\widehat{FDB}\) (2 góc đồng vị và FD//AC)
=> \(\widehat{ACB}=\widehat{FDB}\)
=> tam giác FBD cân tại F
=> FB=FD
Mà FH=FD(tam giác FHD cân tại F)
Nên FB=FH
=> tam giác BHF cân tại F

ta có: EF//BD
FB//ED
suy ra; EB=ED; EF=BD
mà DB=DC suy ra EF=DC
6F1=^B( 2 góc đồng vị)
^B=^D1( 2 góc đồng vị)
suy ra ^F1=^D1
ta có: ^E1=^D2(2 góc đồng vị)
^C=^D2( 2 góc đồng vị)
suy ra ^E1=^C
xét tam giác CDE và tam giác EFA có:
EF=DC(cmt)
^F1=^D1(cmt)
^E1=^C(cmt)
suy ra tam giác CDE=tam giác EFA(g.c.g)
ta có: EF//BD
FB//ED
suy ra; EB=ED; EF=BD
mà DB=DC suy ra EF=DC
6F1=^B( 2 góc đồng vị)
^B=^D1( 2 góc đồng vị)
suy ra ^F1=^D1
ta có: ^E1=^D2(2 góc đồng vị)
^C=^D2( 2 góc đồng vị)
suy ra ^E1=^C
xét tam giác CDE và tam giác EFA có:
EF=DC(cmt)
^F1=^D1(cmt)
^E1=^C(cmt)
suy ra tam giác CDE=tam giác EFA(g.c.g)

a: Xét ΔBNQ có
C là trung điểm của BQ
CA//NQ
Do đó: A là trung điểm của NB
Xét ΔCPM có
B là trung điểm của CP
CA//MP
DO đó: A là trung điểm của CM
Xét tứ giác BMNC có
A là trung điểm chung của BN và MC
nên BMNC là hình bình hành
b: Để ANKM là hình bình hành
nên AM//KN và AN//KM
=>AB//MK và AB=MK
=>ABMK là hình bình hành
=>AI//BM
Xét ΔCBM có
A là trung điểm của CA
AI//BM
DO đó; I là trung điểm của BC

Ta chứng minh được AEDF là hình bình hành Þ AD Ç È = I. I là trung điểm của AD và EF. Suy ra E đối xứng với F qua I